题目内容
设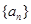 是公比大于1的等比数列,
是公比大于1的等比数列,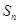 为数列
为数列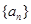 的前
的前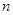 项和.已知
项和.已知 ,且
,且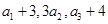 构成等差数列.
构成等差数列.
(Ⅰ)求数列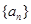 的通项公式;
的通项公式;
(Ⅱ)令 ,求数列
,求数列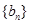 的前
的前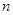 项和
项和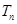 .
.
【答案】
(1)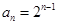 (2)
(2)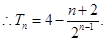
【解析】
试题分析:(1)求等差等比数列的通项公式只要求出基本量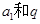 就可以.由已知条件可以构建方程组
就可以.由已知条件可以构建方程组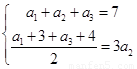 求出
求出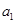 和
和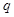 .利用通项公式能够求解通项.(2)因为
.利用通项公式能够求解通项.(2)因为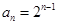 所以
所以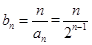 一个等差乘以一个等比,利用错位相减法求和.
一个等差乘以一个等比,利用错位相减法求和.
试题解析:(Ⅰ)由已知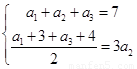 解得
解得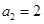 .设数列
.设数列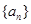 的公比为
的公比为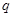 ,由
,由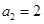 ,可得
,可得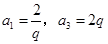 .又
.又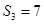 ,可知
,可知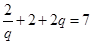 ,即
,即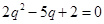 ,
,
解得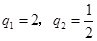 .由题意得
.由题意得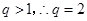 .
.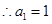 .
.
故数列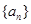 的通项为
的通项为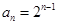 .
6分
.
6分
(Ⅱ)由于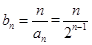 ,所以
,所以
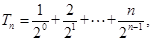
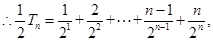
两式相减得:
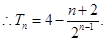 12分
12分
考点:等比数列求通项、数列求和

练习册系列答案
相关题目
 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列 、公差为
、公差为
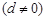 的无穷等差数列.
的无穷等差数列. ,
, 成等比数列,求其公比
成等比数列,求其公比 .
. ,从数列
,从数列 ,从数列
,从数列
 项(设
项(设 )作为一个等比数列的第1项、第2项.求证:当
)作为一个等比数列的第1项、第2项.求证:当 为大于1的正整数时,该数列为
为大于1的正整数时,该数列为 中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列
中取出部分项,并将它们按原来的顺序组成一个数列,称之为数列 、公差为
、公差为
 的无穷等差数列.
的无穷等差数列.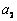 ,
, 成等比数列,求其公比
成等比数列,求其公比 .
. ,从数列
,从数列 ,从数列
,从数列
 项(设
项(设 )作为一个等比数列的第1项、第2项.求证:当
)作为一个等比数列的第1项、第2项.求证:当 为大于1的正整数时,该数列为
为大于1的正整数时,该数列为