题目内容
(坐标系与参数方程选做题)在直角坐标系xoy中,已知曲线C的参数方程是
(θ是参数),若以o为极点,x轴的正半轴为极轴,则曲线C的极坐标方程可写为
|
ρ2+4ρsinθ+3=0
ρ2+4ρsinθ+3=0
.分析:先根据sin2θ+cos2θ=1消去参数θ可得曲线C的直角坐标方程,然后根据x2+y2=ρ2,y=ρsinθ可得极坐标方程.
解答: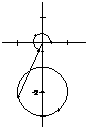 解:在直角坐标系xoy中,
解:在直角坐标系xoy中,
(θ是参数),
∴
根据sin2θ+cos2θ=1可得x2+(y+2)2=1
∴曲线C是以点(0,-2)为圆心,以1为半径的圆,如图
可得x2+(y+2)2=1即x2+y2+4y+3=0
∴曲线C的极坐标方程ρ2+4ρsinθ+3=0
故答案为:ρ2+4ρsinθ+3=0
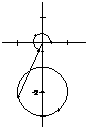 解:在直角坐标系xoy中,
解:在直角坐标系xoy中,
|
∴
|
根据sin2θ+cos2θ=1可得x2+(y+2)2=1
∴曲线C是以点(0,-2)为圆心,以1为半径的圆,如图
可得x2+(y+2)2=1即x2+y2+4y+3=0
∴曲线C的极坐标方程ρ2+4ρsinθ+3=0
故答案为:ρ2+4ρsinθ+3=0
点评:本题主要考查了圆的参数方程转化直角坐标方程,以及直角坐标方程转化成极坐标方程,同时考查了同角三角函数的平方关系,属于基础题.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目