题目内容
（坐标系与参数方程选做题）在极坐标系中，已知点P（2，
），则过点P且平行于极轴的直线的极坐标方程为 ．
| π | 3 |
分析：法一：先将极坐标化成直角坐标表示，过（1，
）且平行于x轴的直线为y=
，再化成极坐标表示即可．
法二：在极坐标系中直接构造直角三角形由其边角关系得方程．
| 3 |
| 3 |
法二：在极坐标系中直接构造直角三角形由其边角关系得方程．
解答：解：法一：先将极坐标化成直角坐标表示，P（2，
）化为（1，
），
过（1，
）且平行于x轴的直线为y=
，再化成极坐标表示，即ρsinθ=
，
法二：在极坐标系中，直接构造直角三角形由其边角关系得方程ρsinθ=
，
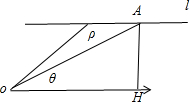
设A（ρ，θ）是直线上的任一点，A到极轴的距离AH=2sin
=
，
直接构造直角三角形由其边角关系得方程ρsinθ=
．
故答案为：ρsinθ=
．
| π |
| 3 |
| 3 |
过（1，
| 3 |
| 3 |
| 3 |
法二：在极坐标系中，直接构造直角三角形由其边角关系得方程ρsinθ=
| 3 |
设A（ρ，θ）是直线上的任一点，A到极轴的距离AH=2sin
| π |
| 3 |
| 3 |
直接构造直角三角形由其边角关系得方程ρsinθ=
| 3 |
故答案为：ρsinθ=
| 3 |
点评：本题考查极坐标与直角坐标的互化，简单曲线的极坐标方程求解，同时考查了分析问题的能力，属于基础题．
练习册系列答案
三点一测快乐周计划系列答案
相关题目