题目内容
指出下列各组命题中,p是q的什么条件?
(1)p:(x-2)(x-3)=0;q:x-2=0.
(2)p:四边形的对角线相等;q:四边形是平行四边形.
(3)p:m<-2,q:方程x2-x-m=0无实根.
(1)p:(x-2)(x-3)=0;q:x-2=0.
(2)p:四边形的对角线相等;q:四边形是平行四边形.
(3)p:m<-2,q:方程x2-x-m=0无实根.
解:(1)∵(x-2)(x-3)=0 x-2=0,
x-2=0,
(x-2)(x-3)=0?x-2=0,
∴p是q的必要不充分条件.
(2)∵四边形的对角线相等 四边形是平行四边形,四边形是平行四边形
四边形是平行四边形,四边形是平行四边形 四边形的对角线相等,
四边形的对角线相等,
∴p是q的既不充分也不必要条件.
(3)∵m<-2⇒方程x2-x-m=0无实根;而方程x2-x-m=0无实根 m<-2.
m<-2.
∴p是q的充分不必要条件.
 x-2=0,
x-2=0,(x-2)(x-3)=0?x-2=0,
∴p是q的必要不充分条件.
(2)∵四边形的对角线相等
 四边形是平行四边形,四边形是平行四边形
四边形是平行四边形,四边形是平行四边形 四边形的对角线相等,
四边形的对角线相等,∴p是q的既不充分也不必要条件.
(3)∵m<-2⇒方程x2-x-m=0无实根;而方程x2-x-m=0无实根
 m<-2.
m<-2.∴p是q的充分不必要条件.
略

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
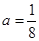 ”是“对任意的正数
”是“对任意的正数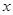 ,
,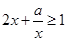 ”的 ( )
”的 ( ) 的充分不必要条件
的充分不必要条件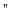
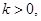 方程
方程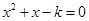 有实根”的否定是:
有实根”的否定是: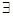
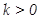 ,方程
,方程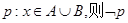 是
是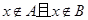
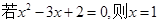 ”的逆否命题为“
”的逆否命题为“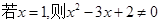 ”
”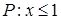 ,条件
,条件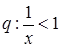 ,则
,则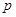 是
是
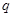 成立的 ( )
成立的 ( )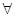 x∈R,x2+1≥2x,则¬P为( )
x∈R,x2+1≥2x,则¬P为( )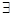 x∈R,x2+1≤2x
x∈R,x2+1≤2x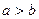 ,则
,则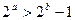 ”的否命题为______
”的否命题为______ 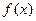 是定义在R上的偶函数,且对任意的
是定义在R上的偶函数,且对任意的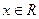 恒有
恒有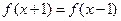 ,
,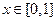 时,
时,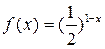 ,则其中所有正确命题的序号
,则其中所有正确命题的序号 是_____________。
是_____________。 ① 2是函数
① 2是函数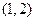 上是减函数,在
上是减函数,在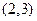 上是增函数;
上是增函数; 最
最 大值是1,最小值是0;④当
大值是1,最小值是0;④当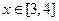 时,
时,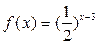 。
。 ,如果连接
,如果连接
 ,则
,则 ”的否命题为“若
”的否命题为“若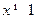 ”;
”;
 ,
,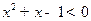 ”的否定是“
”的否定是“
 ,
,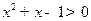 ”;
”;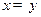 ,则
,则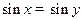 ”的逆否命题为真命题;
”的逆否命题为真命题;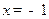 ”是“
”是“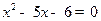 ”的必要不充分条件;
”的必要不充分条件;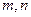 ,则向量
,则向量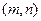 与向量
与向量 的夹角
的夹角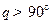 的概率是
的概率是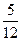 ;
;