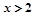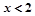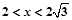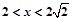题目内容
在△ABC中,角A、B、C所对的边分别是a、b、c,已知cos
=
.
(I)求cosC的值;
(II)若acosB+bcosA=2,求△ABC面积的最大值.
| C |
| 2 |
| ||
| 3 |
(I)求cosC的值;
(II)若acosB+bcosA=2,求△ABC面积的最大值.
(Ⅰ)∵cos
=
,
∴cosC=2cos2
-1=2(
)2-1=
;(7分)
(Ⅱ)∵acosB+bcosA=2,
∴a×
+b×
=2,
∴c=2(9分)
∴4=a2+b2-2ab×
≥2ab-2ab×
=
ab,
∴ab≤
(当且仅当a=b=
时等号成立)(12分)
由cosC=
,得sinC=
(13分)
∴S△ABC=
absinC≤
×
×
=
,
故△ABC的面积最大值为
(14分)
| C |
| 2 |
| ||
| 3 |
∴cosC=2cos2
| C |
| 2 |
| ||
| 3 |
| 1 |
| 9 |
(Ⅱ)∵acosB+bcosA=2,
∴a×
| a2+c2-b2 |
| 2ac |
| c2+b2-a2 |
| 2bc |
∴c=2(9分)
∴4=a2+b2-2ab×
| 1 |
| 9 |
| 1 |
| 9 |
| 16 |
| 9 |
∴ab≤
| 9 |
| 4 |
| 3 |
| 2 |
由cosC=
| 1 |
| 9 |
4
| ||
| 9 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
4
| ||
| 9 |
| ||
| 2 |
故△ABC的面积最大值为
| ||
| 2 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
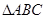 中,角A,B,C分别所对的边为
中,角A,B,C分别所对的边为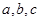 ,且
,且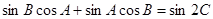 ,
,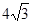 .
.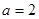 ,求边长
,求边长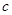 .
.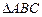 的内角
的内角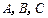 所对的边
所对的边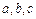 成等比数列,则
成等比数列,则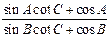 的取值范围是()
的取值范围是()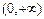
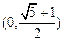
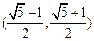

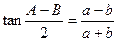 ,其中a,b分别是∠A,∠B的对边,则△ABC是( )
,其中a,b分别是∠A,∠B的对边,则△ABC是( )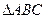 中,角
中,角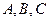 对应的边长为
对应的边长为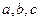 ,若
,若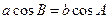 ,则
,则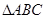 中,
中,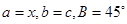 ,若三角形有两解,则x的取值范围是( )
,若三角形有两解,则x的取值范围是( )