题目内容
(本小题满分12分)
已知函数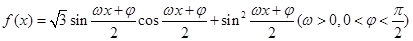 .其图象的两个相邻对称中心的距离为
.其图象的两个相邻对称中心的距离为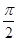 ,且过点
,且过点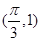 .
.
(I) 函数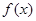 的达式;
的达式;
(Ⅱ)在△ABC中.a、b、c分别是角A、B、C的对边,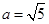 ,
,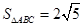 ,角C为锐角。且满
,角C为锐角。且满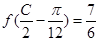 ,求c的值.
,求c的值.
已知函数
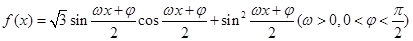 .其图象的两个相邻对称中心的距离为
.其图象的两个相邻对称中心的距离为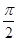 ,且过点
,且过点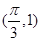 .
.(I) 函数
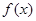 的达式;
的达式;(Ⅱ)在△ABC中.a、b、c分别是角A、B、C的对边,
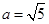 ,
,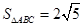 ,角C为锐角。且满
,角C为锐角。且满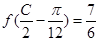 ,求c的值.
,求c的值.(1)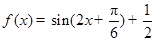 (2)
(2)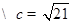
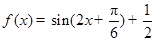 (2)
(2)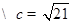
试题分析:解:(Ⅰ)
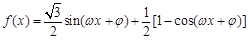
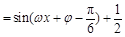 .
. 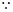 两个相邻对称中心的距离为
两个相邻对称中心的距离为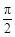 ,则
,则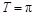 ,
,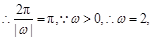
又
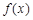 过点
过点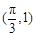 ,
,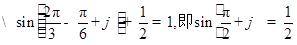 ,
,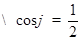 ,
,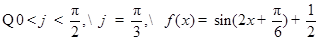 .
. (Ⅱ)
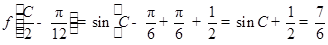 ,
,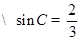 ,
,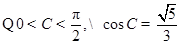 ,
,又
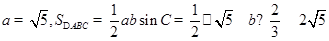 ,
,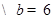 ,
,由余弦定理得
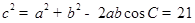 ,
,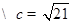 .
.点评:解决的关键是能降函数化为单一函数,同时结合函数的性质来求解参数的值,然后利用三角函数的性质来求解。对于三角方程的求解,主要结合定义域,得到角的范围,然后利用三角函数的图像来得到方程的解,同时结合正弦定理和余弦定理得到求解,属于中档题。

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
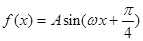 (其中
(其中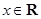 ,
,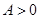 ,
,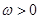 )的最大值为2,最小正周
)的最大值为2,最小正周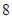 .
.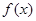 的解析式;
的解析式;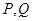 的横坐标依次为
的横坐标依次为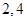 ,
, 为坐标原点,求△
为坐标原点,求△ 的
的 )+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为
)+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为 .
. )=2,求α的值.
)=2,求α的值.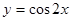 图象上的所有点向左平移
图象上的所有点向左平移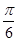 个单位长度,再把所得图像向上平移1个单位长度,所得图象的函数解析式是( )
个单位长度,再把所得图像向上平移1个单位长度,所得图象的函数解析式是( )


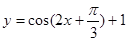
 的图象向左平移
的图象向左平移 个单位,所得图像的解析式是( )
个单位,所得图像的解析式是( )



 .
. 的值;
的值; ,且
,且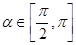 ,求
,求 的值.
的值. ,若
,若 对一切
对一切 恒成立.求实数
恒成立.求实数 的取值范围.
的取值范围. 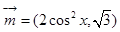 ,
,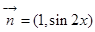 ,函数
,函数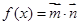 .
.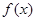 的最小正周期和单调增区间;
的最小正周期和单调增区间;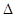
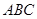 中,
中,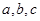 分别是角
分别是角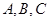 的对边,R为
的对边,R为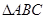 外接圆的半径,且
外接圆的半径,且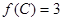 ,
,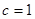 ,
,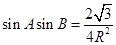 ,且
,且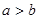 ,求
,求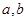 的值.
的值.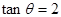 ,则
,则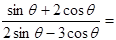 ;
;