题目内容
已知 (x>1),
(x>1),(1)若
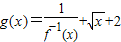 ,求g(x)的最小值;
,求g(x)的最小值;(2)若不等式
 对于一切
对于一切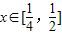 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】分析:(1)先由f(x)求出f-1(x),进而求得g(x),利用基本不等式即可求得g(x)的最小值;
(2)原不等式可化为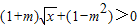 ,令
,令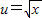 ,则F(u)=(1+m)u+(1-m2)>0在
,则F(u)=(1+m)u+(1-m2)>0在 上恒成立,根据一次函数的性质可得关于m的不等式组,解出即可;
上恒成立,根据一次函数的性质可得关于m的不等式组,解出即可;
解答:解:(1)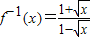 (0<x<1),
(0<x<1),
∴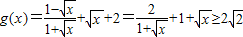 ,等号当且仅当
,等号当且仅当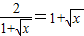 ,即
,即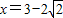 时取得.
时取得.
∴g(x)的最小值为 .
.
(2)不等式即为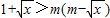 ,也就是
,也就是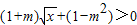 ,
,
令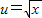 ,则F(u)=(1+m)u+(1-m2)>0在
,则F(u)=(1+m)u+(1-m2)>0在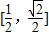 上恒成立,
上恒成立,
∴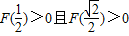 ,解得
,解得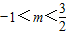 .
.
点评:本题考查函数恒成立问题、反函数的求解及基本不等式求最值,考查转化思想,综合性较强,难度较大.
(2)原不等式可化为
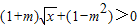 ,令
,令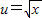 ,则F(u)=(1+m)u+(1-m2)>0在
,则F(u)=(1+m)u+(1-m2)>0在 上恒成立,根据一次函数的性质可得关于m的不等式组,解出即可;
上恒成立,根据一次函数的性质可得关于m的不等式组,解出即可;解答:解:(1)
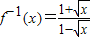 (0<x<1),
(0<x<1),∴
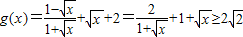 ,等号当且仅当
,等号当且仅当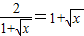 ,即
,即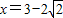 时取得.
时取得.∴g(x)的最小值为
 .
.(2)不等式即为
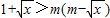 ,也就是
,也就是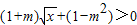 ,
,令
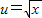 ,则F(u)=(1+m)u+(1-m2)>0在
,则F(u)=(1+m)u+(1-m2)>0在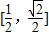 上恒成立,
上恒成立,∴
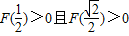 ,解得
,解得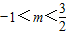 .
.点评:本题考查函数恒成立问题、反函数的求解及基本不等式求最值,考查转化思想,综合性较强,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目