题目内容
有下列叙述:
①集合{x∈N|x=
,a∈N *}中只有四个元素;
②设a>0,将
表示成分数指数幂,其结果是a
;
③已知函数f(x)=
(x≠±1),则f(2)+f(3)+f(4)+f(
)+f(
)+f(
)=3
④设集合A=[0,
,B=[
,1],函数f(x)=
,若x0∈A,且f[f(x0)]∈A,则x0的取值范围是(
,
).
其中所有正确叙述的序号是
①集合{x∈N|x=
| 6 |
| a |
②设a>0,将
| a2 | |||||
|
| 5 |
| 6 |
③已知函数f(x)=
| 1+x2 |
| 1-x2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
④设集合A=[0,
| 1 |
| 2 |
| 1 |
| 2 |
|
| 1 |
| 4 |
| 1 |
| 2 |
其中所有正确叙述的序号是
①
①
.分析:①集合{x∈N|x=
,a∈N *}={1,2,3,6};
②设a>0,将
表示成分数指数幂,其结果是a
;
③函数f(x)=
(x≠±1),则f(2)+f(3)+f(4)+f(
)+f(
)+f(
)=0;
④集合A=[0,
,B=[
,1],函数f(x)=
,x0∈A,且f[f(x0)]∈A,则x0的取值范围是{0}.
| 6 |
| a |
②设a>0,将
| a2 | |||||
|
| 7 |
| 6 |
③函数f(x)=
| 1+x2 |
| 1-x2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
④集合A=[0,
| 1 |
| 2 |
| 1 |
| 2 |
|
解答:解:①∵集合{x∈N|x=
,a∈N *}={1,2,3,6},
∴集合{x∈N|x=
,a∈N *}中只有四个元素,故①正确;
②设a>0,将
表示成分数指数幂,其结果是a
,故②不正确;
③∵函数f(x)=
(x≠±1),
∴f(x)+f(
)=
+
=0,
∴f(2)+f(3)+f(4)+f(
)+f(
)+f(
)=0,故③不正确;
④集合A=[0,
,B=[
,1],函数f(x)=
,
x0∈A,且f[f(x0)]∈A,
则
,∴x0的取值范围是{0},故④不正确.
故答案为:①.
| 6 |
| a |
∴集合{x∈N|x=
| 6 |
| a |
②设a>0,将
| a2 | |||||
|
| 7 |
| 6 |
③∵函数f(x)=
| 1+x2 |
| 1-x2 |
∴f(x)+f(
| 1 |
| x |
| 1+x2 |
| 1-x2 |
1+
| ||
1-
|
∴f(2)+f(3)+f(4)+f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
④集合A=[0,
| 1 |
| 2 |
| 1 |
| 2 |
|
x0∈A,且f[f(x0)]∈A,
则
|
故答案为:①.
点评:本题考查命题的真假判断,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 中只有四个元素;
中只有四个元素; 在其定义域内为增函数;
在其定义域内为增函数; ,则角
,则角 的终边落在第四象限;
的终边落在第四象限; ,且点
,且点 不共线,已知
不共线,已知 ,则△
,则△ 是等腰三角形;
是等腰三角形;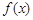 的定义域为
的定义域为 ,则函数
,则函数 的定义域为
的定义域为 .
.