题目内容
有下列叙述:
①集合{x∈N|x=
,a∈N *}中只有四个元素;
②y=tanx在其定义域内为增函数;
③已知α=-6,则角α的终边落在第四象限;
④平面上有四个互异的点A、B、C、D,且点A、B、C不共线,已知(
+
-2
)•(
-
)=0,则△ABC是等腰三角形;
⑤若函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4].
其中所有正确叙述的序号是
①集合{x∈N|x=
| 6 |
| a |
②y=tanx在其定义域内为增函数;
③已知α=-6,则角α的终边落在第四象限;
④平面上有四个互异的点A、B、C、D,且点A、B、C不共线,已知(
| DB |
| DC |
| DA |
| AB |
| AC |
⑤若函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4].
其中所有正确叙述的序号是
①④
①④
.分析:由题意可知,①集合{x∈N|x=
,a∈N *}={6,3,2,}
②y=tanx在(-
π+kπ,
π+kπ),k∈Z为增函数
③已知α=-6,则角α的终边落在第一象限;
④由已知可得(
+
)•(
-
)=0,则可得AB=AC,可判断
⑤由已知可知,在函数f(2x)中有0≤2x≤≤2,从而可求函数的定义域
| 6 |
| a |
②y=tanx在(-
| 1 |
| 2 |
| 1 |
| 2 |
③已知α=-6,则角α的终边落在第一象限;
④由已知可得(
| AB |
| AC |
| AB |
| AC |
⑤由已知可知,在函数f(2x)中有0≤2x≤≤2,从而可求函数的定义域
解答:解:①集合{x∈N|x=
,a∈N *}={6,3,2,},只有四个元素;正确
②y=tanx在(-
π+kπ,
π+kπ),k∈Z为增函数;错误
③已知α=-6,则角α的终边落在第一象限;错误
④由(
+
-2
)•(
-
)=0,可得(
+
)•(
-
)=0,则可得AB=AC,则△ABC是等腰三角形;正确
⑤若函数f(x)的定义域为[0,2],则在函数f(2x)中有0≤2x≤≤2,从而的定义域为[0,1].错误
正确叙述的序号是①④
故答案为:①④
| 6 |
| a |
②y=tanx在(-
| 1 |
| 2 |
| 1 |
| 2 |
③已知α=-6,则角α的终边落在第一象限;错误
④由(
| DB |
| DC |
| DA |
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
⑤若函数f(x)的定义域为[0,2],则在函数f(2x)中有0≤2x≤≤2,从而的定义域为[0,1].错误
正确叙述的序号是①④
故答案为:①④
点评:本题主要考查了集合的表示方法的应用,正切函数的性质的应用,角的终边位置的判断,及向量的基本运算、函数定义域的求解,综合的知识比较多.

练习册系列答案
相关题目
 中只有四个元素;
中只有四个元素; 在其定义域内为增函数;
在其定义域内为增函数; ,则角
,则角 的终边落在第四象限;
的终边落在第四象限; ,且点
,且点 不共线,已知
不共线,已知 ,则△
,则△ 是等腰三角形;
是等腰三角形;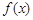 的定义域为
的定义域为 ,则函数
,则函数 的定义域为
的定义域为 .
.