题目内容
P是椭圆
+
=1(a>b>0)上一点,F1、F2是椭圆的左、右焦点,|F1F2|=2c,过P作直线l:x=-
的垂线,垂足为Q,若PQF1F2是平行四边形,则椭圆的离心率取值范围是_
<e<1
<e<1.
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
| 1 |
| 2 |
| 1 |
| 2 |
分析:根据题意得,若PQF1F2是平行四边形,如图,由图可知,椭圆上存在一点,使得它到左准线的距离小于焦距即可,而椭圆上的点到左准线的距离的最小值为左顶点到左准线的距离,从而建立关于e的不等关系,求解即得椭圆的离心率取值范围.
解答: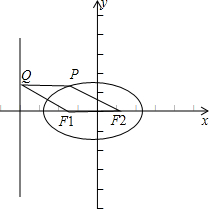 解:若PQF1F2是平行四边形,如图,
解:若PQF1F2是平行四边形,如图,
由图可知,椭圆上存在一点,使得它到左准线的距离小于焦距即可,
而椭圆上的点到左准线的距离的最小值为左顶点到左准线的距离,即a-
,
∴a-
<2c,
即:2c2+ac-a2>0,
从而2e2+e-1>0⇒e>
又椭圆的离心率e<1,
则椭圆的离心率取值范围是
<e<1.
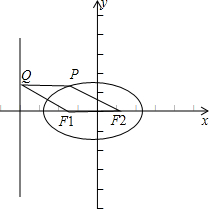 解:若PQF1F2是平行四边形,如图,
解:若PQF1F2是平行四边形,如图,由图可知,椭圆上存在一点,使得它到左准线的距离小于焦距即可,
而椭圆上的点到左准线的距离的最小值为左顶点到左准线的距离,即a-
| a2 |
| c |
∴a-
| a2 |
| c |
即:2c2+ac-a2>0,
从而2e2+e-1>0⇒e>
| 1 |
| 2 |
又椭圆的离心率e<1,
则椭圆的离心率取值范围是
| 1 |
| 2 |
点评:本小题主要考查椭圆的简单性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 给定椭圆C:
给定椭圆C: