题目内容
设 P(x,y),Q(x′,y′) 是椭圆
+
=1(a>0,b>0)上的两点,则下列四个结论:①a2+b2≥(x+y)2;②
+
≥(
+
)2;③
+
≥4;④
+
≤1.其中正确的个数为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| x2 |
| 1 |
| y2 |
| 1 |
| a |
| 1 |
| b |
| a2 |
| x2 |
| b2 |
| y2 |
| xx′ |
| a2 |
| yy′ |
| b2 |
分析:由于点在椭圆上,则点的坐标满足椭圆的方程.
①用(
+
)(a2+b2)替换(a2+b2),
②用(
+
)(
+
)替换(
+
),再根据柯西不等式(a2+b2)(c2+d2)≥(ac+bd)2可得;
③由椭圆的参数方程可求证;
④利用椭圆的有界性来做.
①用(
| x2 |
| a2 |
| y2 |
| b2 |
②用(
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| x2 |
| 1 |
| y2 |
| 1 |
| x2 |
| 1 |
| y2 |
③由椭圆的参数方程可求证;
④利用椭圆的有界性来做.
解答:解:由于 P(x,y)是椭圆
+
=1(a>0,b>0)上的点,则
+
=1,
①(a2+b2)=(a2+b2)(
+
)≥(x+y)2,故①正确;
②(
+
)(
+
)≥(
+
)2,故②也正确;
③由椭圆的参数方程知
+
=
+
=
=
,显然③也正确;
④由于Q(x′,y′) 是椭圆
+
=1(a>0,b>0)上的点.
依据椭圆的有界性知xx′≤a2,yy′≤b2,故
+
≤1,故④也正确.
故答案选D.
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
①(a2+b2)=(a2+b2)(
| x2 |
| a2 |
| y2 |
| b2 |
②(
| 1 |
| x2 |
| 1 |
| y2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| a |
| 1 |
| b |
③由椭圆的参数方程知
| a2 |
| x2 |
| b2 |
| y2 |
| 1 |
| sin2x |
| 1 |
| cos2x |
| 1 |
| sin2x•cos2x |
| 4 |
| sin22x |
④由于Q(x′,y′) 是椭圆
| x2 |
| a2 |
| y2 |
| b2 |
依据椭圆的有界性知xx′≤a2,yy′≤b2,故
| xx′ |
| a2 |
| yy′ |
| b2 |
故答案选D.
点评:本题考查的知识点是,判断命题真假,同时考查了不等式,我们可以根据不等式的性质对四个结论逐一进行判断,可以得到正确的结论.

练习册系列答案
相关题目
 (a>0,b>0)上的两点,则下列四个结论:①a2+b2≥(x+y)2;②
(a>0,b>0)上的两点,则下列四个结论:①a2+b2≥(x+y)2;② ;③
;③ ;④
;④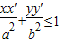 .其中正确的个数为( )
.其中正确的个数为( ) (a>0,b>0)上的两点,则下列四个结论:①a2+b2≥(x+y)2;②
(a>0,b>0)上的两点,则下列四个结论:①a2+b2≥(x+y)2;② ;③
;③ ;④
;④ .其中正确的个数为( )
.其中正确的个数为( )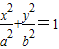 (a>0,b>0)上的两点,则下列四个结论:①a2+b2≥(x+y)2;②
(a>0,b>0)上的两点,则下列四个结论:①a2+b2≥(x+y)2;② ;③
;③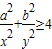 ;④
;④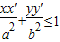 .其中正确的个数为( )
.其中正确的个数为( )