题目内容
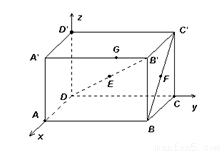
 在如图的长方体中,AD=AA1=1,AB=2,点E在棱AB上移动.
在如图的长方体中,AD=AA1=1,AB=2,点E在棱AB上移动.(1)当E为AB的中点时,求点E到平面ACD1的距离;
(2)AE等于何值时,二面角D1-EC-D的大小为
| π | 4 |
分析:(1)分别以DA,DC,DD1为x,y,z轴建立空间坐标系,求出向量
,
的坐标,设点E到平面ACD1的距离为d,
=(x,y,z)是平面ACD1的法向量,由法向量的性质可求得向量
,则d=
,利用向量运算可得答案;
(2)设AE=l,由(1)知,E(1,l,0),易知平面ECD的法向量
=(0,0,1),设
=(x,y,z)是平面CED1的法向量,由法向量的性质可求得
,由cos
=
可得关于l的方程,解出即可;
| AD1 |
| AC |
| n |
| n |
|
| ||||
|
|
(2)设AE=l,由(1)知,E(1,l,0),易知平面ECD的法向量
| m |
| n |
| n |
| π |
| 4 |
|
| ||||
|
|
解答:解:分别以DA,DC,DD1为x,y,z轴建立空间坐标系,
知E(1,1,0),A(1,0,0),C(0,2,0),D1(0,0,1),
(1)
=(-1,0,1),
=(-1,2,0),
设点E到平面ACD1的距离为d,
=(x,y,z)是平面ACD1的法向量,
由
,得d
,取
=(2,1,2),
而
=(0,1,0),
所以d=
=
为所求;
(2)设AE=l,由(1)知,E(1,l,0),设
=(x,y,z)是平面CED1的法向量,
=(-1,2-l,0),
=(0,-2,1),
而
,即
,取
=(2-l,1,2)
又平面ECD的法向量
=(0,0,1),
由cos
=
,即
=
,
解得l=2-
,即AE=2-
.
知E(1,1,0),A(1,0,0),C(0,2,0),D1(0,0,1),
(1)
| AD1 |
| AC |
设点E到平面ACD1的距离为d,
| n |
由
|
|
| n |
而
| AE |
所以d=
|
| ||||
|
|
| 1 |
| 3 |
(2)设AE=l,由(1)知,E(1,l,0),设
| n |
| EC |
| CD1 |
而
|
|
| n |
又平面ECD的法向量
| m |
由cos
| π |
| 4 |
|
| ||||
|
|
| ||
| 2 |
| 2 | ||
|
解得l=2-
| 3 |
| 3 |
点评:本题考查利用空间向量求二面角、点到平面的距离,考查转化思想,考查学生空间想象能力、逻辑推理能力.

练习册系列答案
相关题目
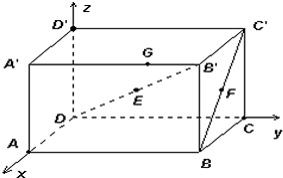 如图,长方体ABCD-A'B'C'D'中,|AD|=3,|AB|=5,|AA'|=3,设E为DB'的中点,F为BC'的中点,在给定的空间直角坐标系D-xyz下,试写出A,B,C,D,A',B',C',D',E,F各点的坐标.
如图,长方体ABCD-A'B'C'D'中,|AD|=3,|AB|=5,|AA'|=3,设E为DB'的中点,F为BC'的中点,在给定的空间直角坐标系D-xyz下,试写出A,B,C,D,A',B',C',D',E,F各点的坐标.

 中,
中,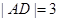 ,
, ,
,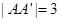 ,设E为
,设E为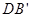 的中点,F为
的中点,F为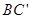 的中点,在给定的空间直角坐标系D-xyz下,试写出A,B,C,D,
的中点,在给定的空间直角坐标系D-xyz下,试写出A,B,C,D, ,
, ,
,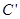 ,
,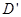 ,E,F各点的坐标.
,E,F各点的坐标.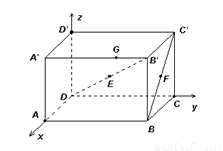
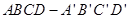 中,
中, ,
,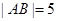 ,
,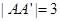 ,设E为
,设E为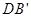 的中点,F为
的中点,F为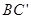 的中点,在给定的空间直角坐标系D-xyz下,试写出A,B,C,D,
的中点,在给定的空间直角坐标系D-xyz下,试写出A,B,C,D, ,
,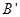 ,
,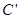 ,
,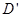 ,E,F各点的坐标.
,E,F各点的坐标.