题目内容
如图,长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,设E为
,设E为![]() 的中点,F为
的中点,F为![]() 的中点,在给定的空间直角坐标系D-xyz下,试写出A,B,C,D,
的中点,在给定的空间直角坐标系D-xyz下,试写出A,B,C,D,![]() ,
,![]() ,
,![]() ,
,![]() ,E,F各点的坐标.
,E,F各点的坐标.

A(3,0,0),B(3,5,0),C(0,5,0),D(0,0,0);![]() (3,0,3),
(3,0,3),![]() (3,5,3),
(3,5,3),![]() (0,5,3),
(0,5,3),![]() (0,0,3);E(
(0,0,3);E(![]() ),F(
),F(![]() ,5,
,5,![]() )
)
解析:
设原点为O,因为A,B,C,D这4个点都在坐标平面 xOy内,
它们的竖坐标都是0,而它们的横坐标和纵坐标可利用![]() ,
,![]() 写出,
写出,
所以 A(3,0,0),B(3,5,0),C(0,5,0),D(0,0,0);
因为平面![]() 与坐标平面xOy平行,且
与坐标平面xOy平行,且![]() ,所以A',B',
,所以A',B',![]() ,D'的竖坐标
,D'的竖坐标
都是3,而它们的横坐标和纵坐标分别与A,B,C,D的相同,所以![]() (3,0,3),
(3,0,3),![]() (3,5,3),
(3,5,3),![]() (0,5,3),
(0,5,3),![]() (0,0,3);
(0,0,3);
由于E分别是![]() 中点,所以它在坐标平面xOy上的射影为DB的中点,从而E的横坐标和纵坐标分别是
中点,所以它在坐标平面xOy上的射影为DB的中点,从而E的横坐标和纵坐标分别是![]() 的
的![]() ,同理E的竖坐标也是
,同理E的竖坐标也是![]() 的竖坐标的
的竖坐标的![]() ,所以E(
,所以E(![]() );
);
由F为![]() 中点可知,F在坐标平面xOy的射影为BC中点,横坐标和纵坐标分别为
中点可知,F在坐标平面xOy的射影为BC中点,横坐标和纵坐标分别为![]() 和5,同理点F在z轴上的投影是AA'中点,故其竖坐标为
和5,同理点F在z轴上的投影是AA'中点,故其竖坐标为![]() ,所以F(
,所以F(![]() ,5,
,5,![]() ).
).

练习册系列答案
相关题目
 如图,长方体中由下面的平面图形围成的是( )
如图,长方体中由下面的平面图形围成的是( ) 在如图的长方体中,AD=AA1=1,AB=2,点E在棱AB上移动.
在如图的长方体中,AD=AA1=1,AB=2,点E在棱AB上移动.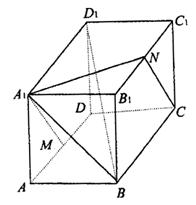
 中
中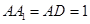 ,
,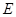 为
为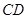 中点.
中点.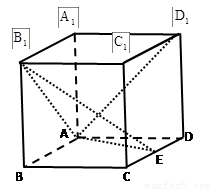
 ;
;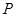 ,使得
,使得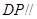 平面
平面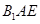 ?若存在,求
?若存在,求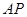 的长;若不存在,说明理由;
的长;若不存在,说明理由;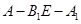 的大小为
的大小为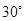 ,求
,求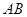 的长.
的长. 中,
中,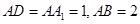 ,点E为AB的中点.
,点E为AB的中点.
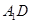 与平面
与平面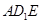 所成的角;
所成的角;  的平面角的正切值.
的平面角的正切值.