题目内容
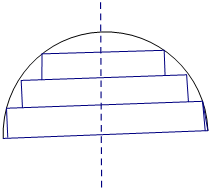 (2012•江苏三模)在一个半径为1的半球材料中截取三个高度均为h的圆柱,其轴截面如图所示,设三个圆柱体积之和为V=f(h).
(2012•江苏三模)在一个半径为1的半球材料中截取三个高度均为h的圆柱,其轴截面如图所示,设三个圆柱体积之和为V=f(h).(1)求f(h)的表达式,并写出h的取值范围是;
(2)求三个圆柱体积之和V的最大值.
分析:(1)根据根据球的截面圆性质,得自下而上三个圆柱的底面半径r1、r2、r3关于h的函数关系式,再结合圆柱的体积公式,可得三个圆柱体积之和为V=f(h)的表达式.根据三个圆柱高度之积小于球半径,得到h的取值范围.
(2)利用导数工具,研究f(h)的单调性,可得f(h)在(0,
)上为增函数,在(
,
)上为减函数,从而得到f(h)的最大值为f(
)=
.
(2)利用导数工具,研究f(h)的单调性,可得f(h)在(0,
| ||
| 14 |
| ||
| 14 |
| 1 |
| 3 |
| ||
| 14 |
| ||
| 7 |
解答:解:(1)设自下而上三个圆柱的底面半径分别为r1、r2、r3,
根据球的截面圆性质,可得r1=
,
r2=
=
,r3=
=
. …(3分)
它们的高均为h,所以体积和等于
V=f(h)=π
h+π
h+π
h
=π[(1-h2)+(1-4h2)+(1-9h2)]h=π(3h-14h3)(6分)
因为三个圆柱高度之积小于球半径,所以0<3h<1,得h的取值范围是(0,
); …(7分)
(2)由f(h)=π(3h-14h3)得f'(h)=π(3-42h2)=3π(1-14h2),…(9分)
又∵h∈(0,
),
∴h∈(0,
)时,f'(h)>0;h∈(
,
)时,f'(h)>0.(11分)
可得f(h)在(0,
)上为增函数,在(
,
)上为减函数,
因此,当h=
时,f(h)取最大值,这个最大值为f(
)=
. …(13分)
答:三个圆柱体积和V的最大值为
. …(14分)
根据球的截面圆性质,可得r1=
| 1-h2 |
r2=
| 1-(2h)2 |
| 1-4h2 |
| 1-(3h)2 |
| 1-9h2 |
它们的高均为h,所以体积和等于
V=f(h)=π
| r | 2 1 |
| r | 2 2 |
| r | 2 3 |
=π[(1-h2)+(1-4h2)+(1-9h2)]h=π(3h-14h3)(6分)
因为三个圆柱高度之积小于球半径,所以0<3h<1,得h的取值范围是(0,
| 1 |
| 3 |
(2)由f(h)=π(3h-14h3)得f'(h)=π(3-42h2)=3π(1-14h2),…(9分)
又∵h∈(0,
| 1 |
| 3 |
∴h∈(0,
| ||
| 14 |
| ||
| 14 |
| 1 |
| 3 |
可得f(h)在(0,
| ||
| 14 |
| ||
| 14 |
| 1 |
| 3 |
因此,当h=
| ||
| 14 |
| ||
| 14 |
| ||
| 7 |
答:三个圆柱体积和V的最大值为
| ||
| 7 |
点评:本题以导数为工具,求三个圆柱体积之和的最大值,着重考查了球的截面圆性质、圆柱体积公式和利用导数研究函数单调性等知识,属于中档题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 (2012•江苏三模)如图,在平面直角坐标系xoy中,圆C:(x+1)2+y2=16,点F(1,0),E是圆C上的一个动点,EF的垂直平分线PQ与CE交于点B,与EF交于点D.
(2012•江苏三模)如图,在平面直角坐标系xoy中,圆C:(x+1)2+y2=16,点F(1,0),E是圆C上的一个动点,EF的垂直平分线PQ与CE交于点B,与EF交于点D.