题目内容
已知随机量X服从正态分布N（3,1），且P（2≤X≤4）=0.6826，则P(X＞4)=
| A．0.1588 | B．0.1587 | C．0.1586 | D．0.1585 |
B
分析：根据题目中：“正态分布N（3，1）”，画出其正态密度曲线图：根据对称性，由（2≤X≤4）的概率可求出P（X＞4）．
解：P（3≤X≤4）=
P（2≤X≤4）=0.3413，
观察上图得，
∴P（X＞4）=0.5-P（3≤X≤4）=0.5-0.3413=0.1587．
故选B．
点评：本题主要考查正态分布曲线的特点及曲线所表示的意义，注意根据正态曲线的对称性解决问题．
解：P（3≤X≤4）=
| 1 |
| 2 |
观察上图得，
∴P（X＞4）=0.5-P（3≤X≤4）=0.5-0.3413=0.1587．
故选B．
点评：本题主要考查正态分布曲线的特点及曲线所表示的意义，注意根据正态曲线的对称性解决问题．
练习册系列答案
名校课堂系列答案
相关题目
，
，则
（ ）
，且
＝0.9544，
＝0.6826，若
＝4，
＝1，则P(5＜x＜6)＝( )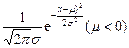
的图象为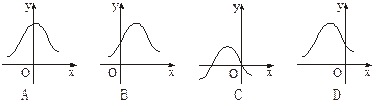
．
服从正态分布
，
,则
（ ）
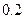
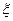～N（175，6
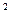）单位：cm，车门应设计的高度至少为 。
）
（
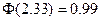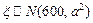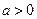，总分满分750分），统计结果显示考试成绩在550分到650分之间的人数约为总人数的
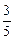，则此次考试成绩高分段（
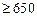）人数约有 ※ 人。