题目内容
设动圆P过点A(-1,0),且与圆B:x2+y2-2x-7=0相切.(Ⅰ)求动圆圆心P的轨迹Ω的方程;
(Ⅱ)设点Q(m,n)在曲线Ω上,求证:直线l:mx+2ny=2与曲线Ω有唯一的公共点;
(Ⅲ)设(Ⅱ)中的直线l与圆B交于点E,F,求证:满足
 的点R必在圆B上.
的点R必在圆B上.
【答案】分析:(Ⅰ)由点A在圆B内,知动圆P与圆B(x-1)2+y2=8内切,由圆B的圆心是B(1,0),半径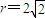 ,知
,知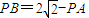 ,由此能求出动圆圆心P的轨迹Ω的方程.
,由此能求出动圆圆心P的轨迹Ω的方程.
(Ⅱ)由点Q(m,n)在曲线Ω上可知:m2+2n2=2.联立直线l与曲线Ω的方程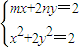 ,得x2-2mx+m2=0,由此能导出直线l与曲线Ω有唯一的公共点.
,得x2-2mx+m2=0,由此能导出直线l与曲线Ω有唯一的公共点.
(Ⅲ)设点E,F的坐标分别为E(x1,y1),F(x2,y2),由题意知x1,x2是由直线l与圆B所得的方程组整理出的方程(m2+4n2)x2-4(m+2n2)x+4-28n2=0的两个不同的实根,再由韦达定理求得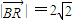 ,故点R在圆B上.
,故点R在圆B上.
解答:解:(Ⅰ)∵点A在圆B内,
∴动圆P与圆B(x-1)2+y2=8内切,
∵圆B的圆心是B(1,0),半径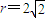 ,
,
∴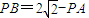 ,
,
即PA+PB=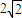 ,
,
由椭圆定义知动圆圆心P的轨迹Ω的方程为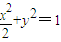 .
.
(Ⅱ)由点Q(m,n)在曲线Ω上可知: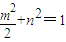 ,即m2+2n2=2.
,即m2+2n2=2.
又联立直线l与曲线Ω的方程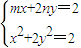 ,
,
得(2m2+4n2)x2-8mx+8-8n2=0,
即x2-2mx+m2=0,
∵x2-2mx+m2=0的两实根相等,
∴直线l与曲线Ω有唯一的公共点.
(Ⅲ)设点E,F的坐标分别为E(x1,y1),F(x2,y2),
则由题意知x1,x2是由直线l与圆B所得的方程组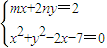
所得方程(m2+4n2)x2-4(m+2n2)x+4-28n2=0的两个不同的实根,
∴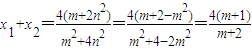 ,
,
∵mx1+2ny1=2,mx2+2ny2=2,
∴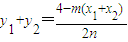 =
=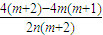 =
=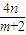 .
.
∴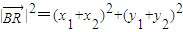
=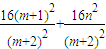
=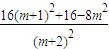
=8,
∴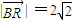 ,
,
故点R在圆B上.
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
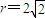 ,知
,知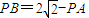 ,由此能求出动圆圆心P的轨迹Ω的方程.
,由此能求出动圆圆心P的轨迹Ω的方程.(Ⅱ)由点Q(m,n)在曲线Ω上可知:m2+2n2=2.联立直线l与曲线Ω的方程
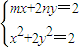 ,得x2-2mx+m2=0,由此能导出直线l与曲线Ω有唯一的公共点.
,得x2-2mx+m2=0,由此能导出直线l与曲线Ω有唯一的公共点.(Ⅲ)设点E,F的坐标分别为E(x1,y1),F(x2,y2),由题意知x1,x2是由直线l与圆B所得的方程组整理出的方程(m2+4n2)x2-4(m+2n2)x+4-28n2=0的两个不同的实根,再由韦达定理求得
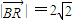 ,故点R在圆B上.
,故点R在圆B上.解答:解:(Ⅰ)∵点A在圆B内,
∴动圆P与圆B(x-1)2+y2=8内切,
∵圆B的圆心是B(1,0),半径
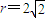 ,
,∴
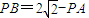 ,
,即PA+PB=
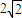 ,
,由椭圆定义知动圆圆心P的轨迹Ω的方程为
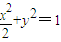 .
.(Ⅱ)由点Q(m,n)在曲线Ω上可知:
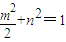 ,即m2+2n2=2.
,即m2+2n2=2.又联立直线l与曲线Ω的方程
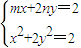 ,
,得(2m2+4n2)x2-8mx+8-8n2=0,
即x2-2mx+m2=0,
∵x2-2mx+m2=0的两实根相等,
∴直线l与曲线Ω有唯一的公共点.
(Ⅲ)设点E,F的坐标分别为E(x1,y1),F(x2,y2),
则由题意知x1,x2是由直线l与圆B所得的方程组
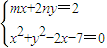
所得方程(m2+4n2)x2-4(m+2n2)x+4-28n2=0的两个不同的实根,
∴
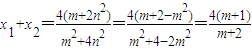 ,
,∵mx1+2ny1=2,mx2+2ny2=2,
∴
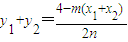 =
=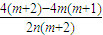 =
=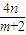 .
.∴
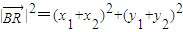
=
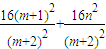
=
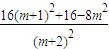
=8,
∴
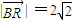 ,
,故点R在圆B上.
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
相关题目
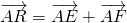 的点R必在圆B上.
的点R必在圆B上.