题目内容
已知动圆P过点(0,
)(a>0)且与直线y=-
相切.
(1)求动圆圆心P的轨迹E的方程;
(2)设直线y=x+2与轨迹E交于点A、B,M是线段AB的中点,过M作x轴的垂线交轨迹E于N.
①证明:轨迹E点N处的切线l与AB平行;
②是否存在实数a,使
•
=0?若存在,求a的值;若不存在,说明理由.
| 1 |
| 4a |
| 1 |
| 4a |
(1)求动圆圆心P的轨迹E的方程;
(2)设直线y=x+2与轨迹E交于点A、B,M是线段AB的中点,过M作x轴的垂线交轨迹E于N.
①证明:轨迹E点N处的切线l与AB平行;
②是否存在实数a,使
| NA |
| NB |
分析:(1)依题意E的轨迹是以为(0,
)(a>0)焦点,y=-
为准线的抛物线方程,由此能求出E的轨迹方程.
(2)设A(x1,y1),B(x2,y2).由
得:ax2-x-2=0.△△=1+8a>0⇒a<-
.再由韦达定理结合题设条件能够求出存在实数a=
,使得
•
=0.
| 1 |
| 4a |
| 1 |
| 4a |
(2)设A(x1,y1),B(x2,y2).由
|
| 1 |
| 8 |
| 7 |
| 8 |
| NA |
| NB |
解答:解:(1)∵动圆P过点(0,
)(a>0)且与直线y=-
相切.
∴E的轨迹是以为(0,
)(a>0)焦点,
y=-
为准线的抛物线方程
所以E的轨迹方程为:y=ax2(a>0)
(2)设A(x1,y1),B(x2,y2).
由
,
得:ax2-x-2=0,△=1+8a>0⇒a<-
,
x1+x2=
,x1x2=-
∴xN=xM=
=
,
∴yN=ax2=
.
①由y′=(ax2)′=2ax,
得:kl=y′|x=xN=2a•
=1,
∴l∥AB.
②假设存在实数a,使得
•
=0,
则
⇒|MN|=
|AB|.
由MN⊥x轴知:|MN|=|
+2-
|=
+2.
又|AB|=
|x1-x2|=
∴(
+2)2=
×2(
+
)⇒a=
或a=-
(舍去)
故存在实数a=
,使得
•
=0.
| 1 |
| 4a |
| 1 |
| 4a |
∴E的轨迹是以为(0,
| 1 |
| 4a |
y=-
| 1 |
| 4a |
所以E的轨迹方程为:y=ax2(a>0)
(2)设A(x1,y1),B(x2,y2).
由
|
得:ax2-x-2=0,△=1+8a>0⇒a<-
| 1 |
| 8 |
x1+x2=
| 1 |
| a |
| 2 |
| a |
∴xN=xM=
| x1+x2 |
| 2 |
| 1 |
| 2a |
∴yN=ax2=
| 1 |
| 4a |
①由y′=(ax2)′=2ax,
得:kl=y′|x=xN=2a•
| 1 |
| 2a |
∴l∥AB.
②假设存在实数a,使得
| NA |
| NB |
则
|
| 1 |
| 2 |
由MN⊥x轴知:|MN|=|
| 1 |
| 2a |
| 1 |
| 4a |
| 1 |
| 4a |
又|AB|=
| 2 |
| 2 |
|
∴(
| 1 |
| 4a |
| 1 |
| 4 |
| 1 |
| a2 |
| 8 |
| a |
| 7 |
| 8 |
| 1 |
| 8 |
故存在实数a=
| 7 |
| 8 |
| NA |
| NB |
点评:本题主要考查直线与圆锥曲线的综合应用能力,综合性强,是高考的重点.本题具体涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要注意合理地进行等价转化.对数学思维的要求比较高,要求学生理解“存在”、“恒成立”,以及运用一般与特殊的关系进行否定,本题有一定的探索性.综合性强,难度大,易出错.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
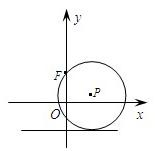 已知动圆P过点
已知动圆P过点 与轨迹W交于A、B两点。
与轨迹W交于A、B两点。 ,求直线
,求直线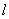 的方程;
的方程; 上是否存在一点Q,使得
上是否存在一点Q,使得 ,并说明理由。
,并说明理由。