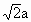题目内容
(理科加试)在极坐标系中,P是曲线ρ=12sinθ上的动点,Q是曲线 上的动点,试求PQ的最大值.
上的动点,试求PQ的最大值.
【答案】分析:将ρ=12sinθ两边同乘以ρ后化成直角坐标方程,再将原极坐标方程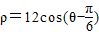 中的三角函数利用差角公式展开后,两边同乘以ρ后化成直角坐标方程,利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换,最后利用直角坐标方程进行求解.
中的三角函数利用差角公式展开后,两边同乘以ρ后化成直角坐标方程,利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换,最后利用直角坐标方程进行求解.
解答:解:∵ρ=12sinθ∴ρ2=12ρsinθ
∴x2+y2-12y=0即x2+(y-6)2=36
又∵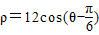
∴
∴x2+y2-6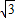 x-6y=0
x-6y=0
∴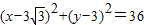
∴PQmax=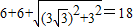 .
.
点评:本题考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.属于基础题.
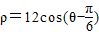 中的三角函数利用差角公式展开后,两边同乘以ρ后化成直角坐标方程,利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换,最后利用直角坐标方程进行求解.
中的三角函数利用差角公式展开后,两边同乘以ρ后化成直角坐标方程,利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换,最后利用直角坐标方程进行求解.解答:解:∵ρ=12sinθ∴ρ2=12ρsinθ
∴x2+y2-12y=0即x2+(y-6)2=36
又∵
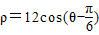
∴

∴x2+y2-6
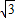 x-6y=0
x-6y=0∴
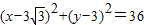
∴PQmax=
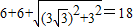 .
.点评:本题考查点的极坐标和直角坐标的互化,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
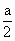 被曲线ρ=2acosθ所截,则截得的弦长为
被曲线ρ=2acosθ所截,则截得的弦长为