题目内容
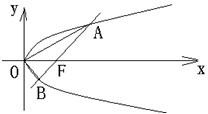过直角坐标平面xOy中的抛物线y2=2px（p＞0）的焦点F作一条倾斜角为| π | 4 |
（1）用p表示A，B之间的距离；
（2）证明：∠AOB的大小是与p无关的定值，并求出这个值．
分析：（1）焦点F（1，0），过抛物线的焦点且倾斜角为
的直线方程是y=x-
由
?x2-3px+
=0，由此能用p表示A，B之间的距离．
（2）由题设知cos∠AOB=
=
=
=
=-
，由此可知∠AOB的大小是与p无关的定值，并能求出这个定值．
| π |
| 4 |
| p |
| 2 |
|
| p2 |
| 4 |
（2）由题设知cos∠AOB=
| |AO|2+|BO|2-|AB|2 |
| 2|AO||BO| |
| xA2+yA2+xB2+yB2-(xA-xB)2-(yA-yB)2 | ||
2
|
| xAxB+yAyB | ||
|
2xAxB-
| ||||
|
3
| ||
| 41 |
解答：解：（1）焦点F（1，0），过抛物线的焦点且倾斜角为
的直线方程是y=x-
由
?x2-3px+
=0?xA+xB=3p，xAxB=
?|AB|=xA+xB+p=4p
（或|AB|=
=4p）
（2）cos∠AOB=
=
=
=
=-
∴∠AOB的大小是与p无关的定值，∠AOB=π-arccos
．
| π |
| 4 |
| p |
| 2 |
由
|
| p2 |
| 4 |
| p2 |
| 4 |
（或|AB|=
| 2p | ||
sin2
|
（2）cos∠AOB=
| |AO|2+|BO|2-|AB|2 |
| 2|AO||BO| |
=
| xA2+yA2+xB2+yB2-(xA-xB)2-(yA-yB)2 | ||
2
|
=
| xAxB+yAyB | ||
|
=
2xAxB-
| ||||
|
=-
3
| ||
| 41 |
∴∠AOB的大小是与p无关的定值，∠AOB=π-arccos
3
| ||
| 41 |
点评：本题考查圆锥曲线的性质和应用，解题时要仔细审题，认真解答．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
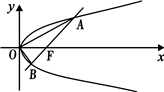过直角坐标平面xOy中的抛物线y2=2px（p＞0）的焦点F作一条倾斜角为
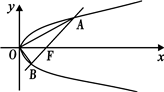过直角坐标平面xOy中的抛物线y2=2px（p＞0）的焦点F作一条倾斜角为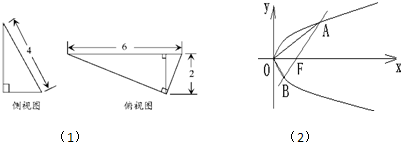
（2005•上海模拟）本题共有2个小题，第1小题满分8分，第2小题满分6分