Question

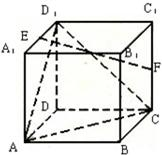如图，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，E、F分别为A₁D₁和CC₁的中点．
（1）求证：EF∥平面ACD₁；
（2）求面EFB与底面ABCD所成的锐二面角余弦值的大小．

Answer 1

分析：如图分别以DA、DC、DD₁所在的直线为x轴、y轴、z轴建立空间直角坐标系D-xyz，先写出各点坐标：
（1）取AD₁中点G，则G（1，0，1），

CG

=（1，-2，1），又

EF

=（-1，2，-1），证明

EF

与

CG

共线即可；
（2）设

n

=(x，y，z)面EFB的一个法向量，再取底面ABCD的一个法向量

m

=(0，0，1)，两个法向量的夹角就是所成的锐二面角的大小，从而求解．

解答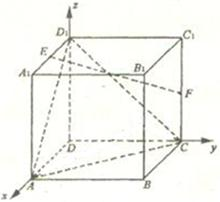：解：如图分别以DA、DC、DD₁所在的直线为x轴、y轴、z轴建立空间直角坐标系D-xyz，由已知得D（0，0，0）、A（2，0，0）、B（2，2，0）、
C（0，2，0）、B₁（2，2，2）、D₁（0，0，2）、E（1，0，2）、F（0，2，1）．
（1）取AD₁中点G，则G（1，0，1），

CG

=（1，-2，1），又

EF

=（-1，2，-1），由

EF

=-

CG

，
∴

EF

与

CG

共线．
从而EF∥CG，
∵CG?平面ACD₁，EF?平面ACD₁，
∴EF∥平面ACD₁．（6分）
（2）设

n

=(x，y，z)面EFB的一个法向量，
由

n

⊥

FE

，

n

⊥

FB

得

x=1 y= 3 2 z=2

，
故可取

n

=(1，

3

2

，2)，（8分）
取底面ABCD的一个法向量

m

=(0，0，1)，
由cos?

m

，n

?=

m •n

| m || •n |

=

4

29

=

4 29

29

，
所成的锐二面角余弦值的大小为

4 29

29

．（12分）

点评：此题考查直线与平面平行的判断及平面与平面垂直的夹角问题，因为此题是正方体，图形比较特殊，利用向量法求解会简单些，此类立体几何题是每年高考必考的一道大题，平时要注意这方面的题．