题目内容
1.函数y1=|x+2|-|x一1|与函数y2=a的图象没有公共点.求实数a的范围.分析 分别画出分别画出y1和y2的图象,由图象可知函数y1=|x+2|-|x一1|与函数y2=a的图象没有公共点a的取值范围.
解答  解:y1=|x+2|-|x-1|=$\left\{\begin{array}{l}{3,x≥1}\\{2x+1,-2<x<1}\\{-3,x≤-2}\end{array}\right.$,
解:y1=|x+2|-|x-1|=$\left\{\begin{array}{l}{3,x≥1}\\{2x+1,-2<x<1}\\{-3,x≤-2}\end{array}\right.$,
分别画出y1和y2的图象,如图所示,
∵函数y1=|x+2|-|x一1|与函数y2=a的图象没有公共点,
∴a>3或a<-3,
∴实数a的范围为(-∞,-3)∪(3,+∞).
点评 本题考查了函数图象的画法和函数图象的性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.判断下列对应关系是否为函数,若不是,说明理由:
(1)x→$\frac{2}{x}$,x∈R;
(2)x→y,y2=x,x∈N,y∈R;
(3)y=$\sqrt{x-2}$+$\sqrt{1-x}$.
(1)x→$\frac{2}{x}$,x∈R;
(2)x→y,y2=x,x∈N,y∈R;
(3)y=$\sqrt{x-2}$+$\sqrt{1-x}$.
9.已知中心在原点的双曲线C的右焦点为F(4,0),离心率等于$\frac{4}{3}$,则C的方程是( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{7}$=1 | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{25}$=1 |
 函数
函数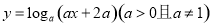 的图象必过定点
的图象必过定点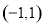 ;命题
;命题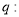 如果函数
如果函数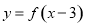 的图象关于原点对称,那么函数
的图象关于原点对称,那么函数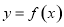 的图象关于点
的图象关于点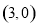 对称,则命题
对称,则命题 为__________(填“真”或“假”).
为__________(填“真”或“假”). 中,有一个内角为30°,“
中,有一个内角为30°,“ ”是“
”是“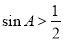 ”的( )条件.
”的( )条件. 的定义域为____________.
的定义域为____________.