题目内容
13.若tanα=-3,且$\frac{π}{2}$<α<π,则$\frac{sin2α-2co{s}^{2}α}{sin(α-\frac{π}{4})}$=-$\frac{2\sqrt{5}}{5}$.分析 由条件利用同角三角函数的基本关系求得cosα的值,再利用二倍角公式、两角差的正弦公式化简要求的式子,可得结果.
解答 解:∵tanα=$\frac{sinα}{cosα}$=-3,sin2α+cos2α=1,且$\frac{π}{2}$<α<π,
∴cosα=-$\frac{\sqrt{10}}{10}$,
则$\frac{sin2α-2co{s}^{2}α}{sin(α-\frac{π}{4})}$=$\frac{2sinαcosα-{2cos}^{2}α}{\frac{\sqrt{2}}{2}sinα-\frac{\sqrt{2}}{2}cosα}$=2$\sqrt{2}$cosα=-$\frac{2\sqrt{5}}{5}$,
故答案为:-$\frac{2\sqrt{5}}{5}$.
点评 本题主要考查同角三角函数的基本关系,二倍角公式、两角差的正弦公式,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
5.某地对农户抽样调查,结果如下:电冰箱拥有率为55%,电视机拥有率为55%,洗衣机拥有率为65%,拥有上述三种电器的任意两种的占35%,三种电器齐全的为25%,那么一种电器也没有的农户所占比例是( )
| A. | 20% | B. | 10% | C. | 15% | D. | 12% |
20.己知直线l1与l2均过点M(4,2),且l1⊥l2,l1与2分别和x,y轴交于A,B两点,点P是线段AB的中点,则|OP|的最小值是( )
| A. | 2 | B. | 5 | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{13}}{2}$ |
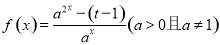 是定义域为
是定义域为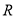 的奇函数.
的奇函数.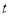 的值;
的值;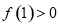 ,求使不等式
,求使不等式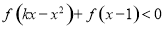 对一切
对一切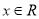 恒成立的实数
恒成立的实数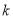 的取值范围.
的取值范围.