题目内容
下列命题中假命题 是
- A.离心率为
 的双曲线的两条渐近线互相垂直
的双曲线的两条渐近线互相垂直 - B.过点(1,1)且与直线
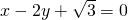 垂直的直线方程是2x+y-3=0
垂直的直线方程是2x+y-3=0 - C.抛物线y2=2x的焦点到准线的距离为1
- D.
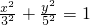 的两条准线之间的距离为
的两条准线之间的距离为
D
分析:A设出双曲线的标准方程,则可表示出其渐近线的方程,根据离心率为 ,推断出其斜率之积为-1进而求得a两条渐近线互相垂直.
,推断出其斜率之积为-1进而求得a两条渐近线互相垂直.
B设与直线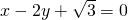 垂直的直线的方程,把点(1,1)的坐标代入求出c值,即得所求的直线的方程.
垂直的直线的方程,把点(1,1)的坐标代入求出c值,即得所求的直线的方程.
C根据抛物线的方程求得抛物线的焦点坐标和准线的方程,进而利用点到直线的距离求得焦点到准线的距离.
D先据标准方程求出a2、b2,计算c2,两准线间的距离为
解答:对于A:设双曲线方程为 ,则双曲线的渐近线方程为y=±
,则双曲线的渐近线方程为y=± x
x
根据离心率为 ,推断出其斜率之积为-1进而两条渐近线互相垂直,故正确;
,推断出其斜率之积为-1进而两条渐近线互相垂直,故正确;
B:设所求的直线方程为2x+y+c=0,把点(1,1)的坐标代入得 2+1+c=0,
∴c=-3,
故所求的直线的方程为2x+y-3=0,故正确;
C:根据题意可知焦点F( ,0),准线方程x=-
,0),准线方程x=- ,
,
∴焦点到准线的距离是1,故正确.
D:a=3,b=5,∴c2=41, =
=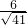 ,∴两准线间的距离为
,∴两准线间的距离为 =
=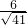
故错.
故选 D.
点评:本小题主要考查圆锥曲线的共同特征、抛物线的简单性质.考查了学生对抛物线标准方程的理解和运用,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
分析:A设出双曲线的标准方程,则可表示出其渐近线的方程,根据离心率为
 ,推断出其斜率之积为-1进而求得a两条渐近线互相垂直.
,推断出其斜率之积为-1进而求得a两条渐近线互相垂直.B设与直线
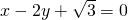 垂直的直线的方程,把点(1,1)的坐标代入求出c值,即得所求的直线的方程.
垂直的直线的方程,把点(1,1)的坐标代入求出c值,即得所求的直线的方程.C根据抛物线的方程求得抛物线的焦点坐标和准线的方程,进而利用点到直线的距离求得焦点到准线的距离.
D先据标准方程求出a2、b2,计算c2,两准线间的距离为

解答:对于A:设双曲线方程为
 ,则双曲线的渐近线方程为y=±
,则双曲线的渐近线方程为y=± x
x根据离心率为
 ,推断出其斜率之积为-1进而两条渐近线互相垂直,故正确;
,推断出其斜率之积为-1进而两条渐近线互相垂直,故正确;B:设所求的直线方程为2x+y+c=0,把点(1,1)的坐标代入得 2+1+c=0,
∴c=-3,
故所求的直线的方程为2x+y-3=0,故正确;
C:根据题意可知焦点F(
 ,0),准线方程x=-
,0),准线方程x=- ,
,∴焦点到准线的距离是1,故正确.
D:a=3,b=5,∴c2=41,
 =
=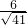 ,∴两准线间的距离为
,∴两准线间的距离为 =
=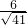
故错.
故选 D.
点评:本小题主要考查圆锥曲线的共同特征、抛物线的简单性质.考查了学生对抛物线标准方程的理解和运用,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,那么下列命题中假命题是( )
,那么下列命题中假命题是( )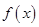 既不是奇函数,也不是偶函数 B.
既不是奇函数,也不是偶函数 B.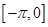 上恰有一个零点
上恰有一个零点 上是增函数
上是增函数 的双曲线的两条渐近线互相垂直
的双曲线的两条渐近线互相垂直 垂直的直线方程是2x+y-3=0
垂直的直线方程是2x+y-3=0 的两条准线之间的距离为
的两条准线之间的距离为