题目内容
下列命题中假命题是( )
| A.?x>0,有ln2x+lnx+1>0 |
| B.?α,β∈R,使cos(α+β)=cosα+cosβ |
| C.“a2<b2”是“a<b”的必要不充分条件 |
| D.?m∈R,使f(x)=(m-1)xm2-4m+3是幂函数,且在(0,+∞)上递减 |
对于A,令lnx=t则ln2x+lnx+1=t2+t+1,因为△=-3<0,所以t2+t+1>0,所以ln2x+lnx+1>0,所以A正确;
对于B,当α=
,β=-
时,有cos(α+β)=cosα+cosβ,所以?α,β∈R,使cos(α+β)=cosα+cosβ,所以B正确;
对于C,例如a=-2,b=1满足“a<b”推不出“a2<b2”,所以“a2<b2”不是“a<b”的必要不充分条件,所以C不正确;
对于D,使f(x)=(m-1)xm2-4m+3是幂函数,且在(0,+∞)上递减,需要
所以m=2,所以D正确
故选C
对于B,当α=
| π |
| 3 |
| π |
| 3 |
对于C,例如a=-2,b=1满足“a<b”推不出“a2<b2”,所以“a2<b2”不是“a<b”的必要不充分条件,所以C不正确;
对于D,使f(x)=(m-1)xm2-4m+3是幂函数,且在(0,+∞)上递减,需要
|
故选C

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 ,那么下列命题中假命题是( )
,那么下列命题中假命题是( )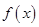 既不是奇函数,也不是偶函数 B.
既不是奇函数,也不是偶函数 B.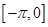 上恰有一个零点
上恰有一个零点 上是增函数
上是增函数 的双曲线的两条渐近线互相垂直
的双曲线的两条渐近线互相垂直 垂直的直线方程是2x+y-3=0
垂直的直线方程是2x+y-3=0 的两条准线之间的距离为
的两条准线之间的距离为