题目内容
(本小题满分12分)
已知直线 经过抛物线
经过抛物线 的焦点,且与抛物线交于
的焦点,且与抛物线交于 两点,点
两点,点 为坐标原点.
为坐标原点.

(Ⅰ)证明: 为钝角.
为钝角.
(Ⅱ)若 的面积为
的面积为 ,求直线
,求直线 的方程;
的方程;
【答案】
(I)见解析;(Ⅱ)直线方程为 。
。
【解析】
试题分析:(I)依题意设直线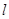 的方程为:
的方程为: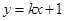 (
(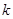 必存在)
必存在)
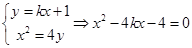 ,
,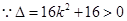
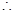 设直线
设直线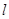 与抛物线的交点坐标为
与抛物线的交点坐标为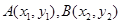 ,则有
,则有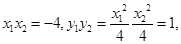
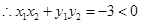 ,依向量的数量积定义,
,依向量的数量积定义,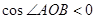 即证
即证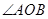 为钝角
为钝角
(Ⅱ) 由(I)可知: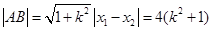 ,
,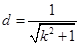 ,
,
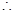
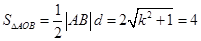 ,
,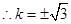 ,
,  直线方程为
直线方程为
考点:本题主要考查直线与抛物线的位置关系;弦长公式。
点评:利用一元二次方程根与系数的关系,结合数量积的坐标运算,将问题进行了等价转化。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目