题目内容
已知函数
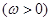 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减;如图,四边形
上单调递减;如图,四边形 中,
中, ,
, ,
, 为
为 的内角
的内角 的对边,
的对边,
且满足 .
.

(Ⅰ)证明: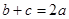 ;
;
(Ⅱ)若 ,设
,设 ,
, ,
,
 ,求四边形
,求四边形 面积的最大值.
面积的最大值.
【答案】
(1)正弦定理的运用根据边角的转换来得到证明。
(2) 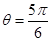 时取最大值,
时取最大值,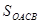 的最大值为
的最大值为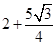
【解析】
试题分析:解:(Ⅰ)由题意知: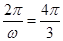 ,解得:
,解得: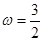 , 2分
, 2分
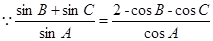
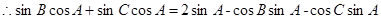
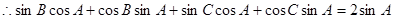
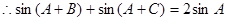 4分
4分
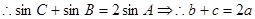 6分
6分
(Ⅱ)因为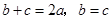 ,所以
,所以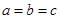 ,所以
,所以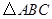 为等边三角形
为等边三角形
 8分
8分
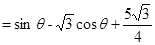
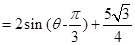 , 10分
, 10分
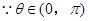 ,
,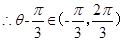 ,
,
当且仅当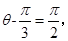 即
即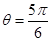 时取最大值,
时取最大值,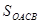 的最大值为
的最大值为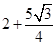 12分
12分
考点:解三角形以及三角函数性质的运用
点评:解决的关键是利用三角函数的性质得到最值,属于基础题。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
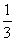
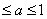 , 若
, 若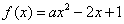 在区间
在区间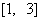 上的最大值为
上的最大值为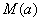 , 最小值为
, 最小值为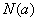 , 令
, 令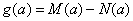 .
.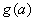 的函数表达式;
的函数表达式;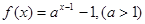 的反函数为
的反函数为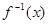 .
. 在区间
在区间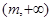 上单增,求实数
上单增,求实数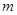 的取值范围;
的取值范围;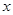 的方程
的方程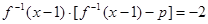 在
在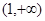 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数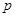 的取值范围.
的取值范围.
 , 若
, 若 在区间
在区间 上的最大值为
上的最大值为 , 最小值为
, 最小值为 , 令
, 令 .
. 的函数表达式;
的函数表达式;