题目内容
一个篮球运动员投篮一次得3分的概率为 ,得2分的概率为
,得2分的概率为 ,不得分的概率为
,不得分的概率为 (
( 、
、 、
、 ),已知他投篮一次得分的数学期望为2(不计其它得分情况),则
),已知他投篮一次得分的数学期望为2(不计其它得分情况),则 的最大值为:
的最大值为:
A. | B. | C.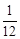 | D. |
D
解析试题分析:利用数学期望的概念,建立等式,再利用基本不等式,即可求得ab的最大值解:由题意,投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c(a、b、c∈(0,1)),∴3a+2b=2,∴2≥2 ∴ab≤
∴ab≤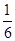 (当且仅当a=
(当且仅当a=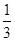 ,b=
,b=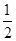 时取等号)】∴ab的最大值为
时取等号)】∴ab的最大值为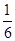 故选D.
故选D.
考点:基本不等式求最值
点评:本题考查数学期望,考查利用基本不等式求最值,利用数学期望的概念,建立等式是关键.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
若直线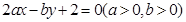 被圆
被圆 截得的弦长为4,则
截得的弦长为4,则 的最小值是( )
的最小值是( )
| A.16 | B.9 | C.12 | D.8 |
在直角坐标系中,定义两点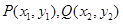 之间的“直角距离”为
之间的“直角距离”为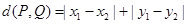 ,
,
现给出四个命题:
①已知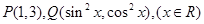 ,则
,则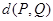 为定值;
为定值;
②用 表示
表示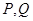 两点间的“直线距离”,那么
两点间的“直线距离”,那么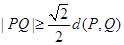 ;
;
③已知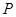 为直线
为直线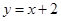 上任一点,
上任一点,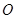 为坐标原点,则
为坐标原点,则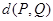 的最小值为
的最小值为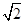 ;
;
④已知 三点不共线,则必有
三点不共线,则必有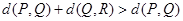 .
.
| A.②③ | B.①④ | C.①② | D.①②④ |
设 、
、 为正数,则
为正数,则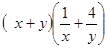 的最小值为( )
的最小值为( )
A. | B.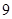 | C.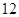 | D. |
若一个矩形的对角线长为常数 ,则其面积的最大值为 ( )
,则其面积的最大值为 ( )
A. | B. | C. | D. |
已知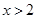 ,则函数
,则函数 的最小值是( )
的最小值是( )
| A.5 | B.4 | C.8 | D.6 |
函数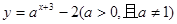 的图像恒过定点A,且点A在直线
的图像恒过定点A,且点A在直线 上
上 ,则
,则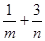 的最小值为( )
的最小值为( )
| A.12 | B.10 | C.8 | D.14 |
若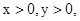 且
且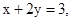 则
则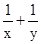 的最小值为( )
的最小值为( )
A.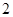 | B.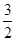 | C.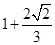 | D. |
设正实数 满足
满足 ,则当
,则当 取得最大值时,
取得最大值时, 的最大值为( )
的最大值为( )
A. | B. | C. | D. |