题目内容
已知点P(2cos α,2sin α)和Q(a,0),O为坐标原点.当α∈(0,π)时.
(1)若存在点P,使得OP⊥PQ,求实数a的取值范围;
(2)如果a=-1,求向量![]() 的夹角θ的最大值.
的夹角θ的最大值.
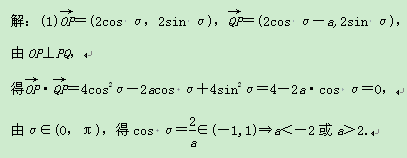
(2)解法一:(![]() 向量坐标法)当a=-1时,
向量坐标法)当a=-1时,
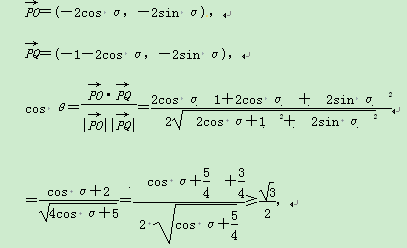 ,
,
当cos α+![]() =
=![]() ,即cos α=-
,即cos α=-![]() ,
,
α=![]() π∈(0,π)时,取等号.
π∈(0,π)时,取等号.
又∵cos θ在θ∈(0,π)上是减函数,∴θmax=![]() .
.
解法二:(余弦定理法)
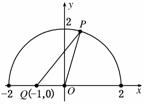
如图,|OQ|=1,|OP|=2,
设|PQ|=t,则cos θ=![]()
![]()
又∵c![]() os θ在θ∈(0,
os θ在θ∈(0,![]() )上是减函数,
)上是减函数,
∴θmax=![]() ,此时PQ⊥OQ,cos α=-
,此时PQ⊥OQ,cos α=-![]() ,α=
,α=![]() π
π![]() ∈(0,π).
∈(0,π).

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
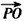 与
与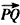 的夹角为θ,求证:cosθ≥
的夹角为θ,求证:cosθ≥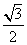 。
。