题目内容
已知点P(2cosα,2sinα)和Q( a,0 ),O为坐标原点.当α∈(0,π)时.(Ⅰ)若存在点P,使得OP⊥PQ,求实数a的取值范围;
(Ⅱ) 如果a=-1,求向量
| PO |
| PQ |
分析:(Ⅰ)先求出
,
的坐标代入x1x2+y1y2=0即可求出实数a的取值范围;
(Ⅱ)把a=-1代入
,
的坐标,进一步求出两个向量的模及他们的数量积,然后代入公式cosθ=
即可求解.
| OP |
| PQ |
(Ⅱ)把a=-1代入
| OP |
| PQ |
| ||||
|
|
解答:解:(Ⅰ)
=(2cosα,2sinα)
=(a-2cosα,-2sinα),
由OP⊥PQ,得
•
=4cos2α-2acosα+4sin2α=4-2acosα=0,
由α∈(0,π),得cosα=
∈(-1,1),
∴a<-2或a>2.(7分)
(Ⅱ)当a=-1时,
=(-2cosα,-2sinα),
=(-1-2cosα,-2sinα),
当cosα+
=
,即cosα=-
,α=
π∈(0,π)时,取等号.
又∵cosθ在θ∈(0,π)上是减函数,
∴θmax=
.(8分)
| OP |
| PQ |
由OP⊥PQ,得
| OP |
| QP |
由α∈(0,π),得cosα=
| 2 |
| a |
∴a<-2或a>2.(7分)
(Ⅱ)当a=-1时,
| PO |
| PQ |
|
当cosα+
| 5 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 2 |
| 3 |
又∵cosθ在θ∈(0,π)上是减函数,
∴θmax=
| π |
| 6 |
点评:如果已知向量的坐标,求向量的夹角,我们可以分别求出两个向量的坐标,进一步求出两个向量的模及他们的数量积,然后代入公式cosθ=
即可求解
| ||||
|
|

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
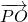 与
与 的夹角为θ,求证:cosθ≥
的夹角为θ,求证:cosθ≥ .
. 与
与 的夹角θ的最大值.
的夹角θ的最大值. 与
与 的夹角为θ,求证:cosθ≥
的夹角为θ,求证:cosθ≥ .
.