题目内容
已知点P(2cosα,2sinα)和Q( a,0 ),O为坐标原点.当α∈(0,π)时,(Ⅰ)若存在点P,使得PO⊥PQ,求实数a的取值范围;
(Ⅱ) 如果a=-1,设向量
| PO |
| PQ |
| ||
| 2 |
分析:(Ⅰ)先写出向量的坐标
,
,由题意可得
⊥
,利用向量垂直的条件得到cosα=
.利用-1≤cosα≤1即可求出实数a的取值范围;
(Ⅱ) 如果a=-1,
=(-1-2cosα,-2sinα),利用向计算公式得夹角余弦值cosθ=
=
,设
=t,利用换元法即可求得其范围,从而得出cosθ≥
.
| PO |
| PQ |
| PO |
| PQ |
| 2 |
| a |
(Ⅱ) 如果a=-1,
| PQ |
| ||||
|
|
| cosα+2 | ||
|
| 5+4cosα |
| ||
| 2 |
解答:解:(Ⅰ)
=(-2cosα,-2sinα),
=(a-2cosα,-2sinα),
由题意可得
⊥
,
∴(-2cosα,-2sinα)•(a-2cosα,-2sinα)=(-2cosα)•(a-2cosα)+4sin2α=0,
∴cosα=
.
当α∈(0,π)时,-1≤cosα≤1,∴-1≤
≤1,
∴a≤-2,或 a≥2,故实数a的取值范围为 (-∞,-2]∪[2,+∞).
(Ⅱ) 如果a=-1,
=(-1-2cosα,-2sinα),
cosθ=
=
=
=
设
=t,则cosα=
,
∴
=
=
≥
,
∴cosθ≥
.
| PO |
| PQ |
由题意可得
| PO |
| PQ |
∴(-2cosα,-2sinα)•(a-2cosα,-2sinα)=(-2cosα)•(a-2cosα)+4sin2α=0,
∴cosα=
| 2 |
| a |
当α∈(0,π)时,-1≤cosα≤1,∴-1≤
| 2 |
| a |
∴a≤-2,或 a≥2,故实数a的取值范围为 (-∞,-2]∪[2,+∞).
(Ⅱ) 如果a=-1,
| PQ |
cosθ=
| ||||
|
|
| (-2cosα,-2sinα)•(-1-2cosα,-2sinα) |
| |(-2cosα,-2sinα)|•|(-1-2cosα,-2sinα)| |
| 2cosα+4 | ||
2
|
=
| cosα+2 | ||
|
设
| 5+4cosα |
| t 2-5 |
| 4 |
∴
| cosα+2 | ||
|
| ||
| t |
| t 2+3 |
| 4t |
| ||
| 2 |
∴cosθ≥
| ||
| 2 |
点评:本小题主要考查数量积判断两个平面向量的垂直关系、数量积表示两个向量的夹角、基本不等式等基础知识,考查运算求解能力,化归与转化思想.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
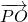 与
与 的夹角为θ,求证:cosθ≥
的夹角为θ,求证:cosθ≥ .
. 与
与 的夹角θ的最大值.
的夹角θ的最大值. 与
与 的夹角为θ,求证:cosθ≥
的夹角为θ,求证:cosθ≥ .
.