题目内容
5.已知f(x)为定义在R上的奇函数,且当x>0时,f(x)=-2x-1(1)求出函数f(x)的解析式;
(2)当x∈[0,1]时,求出f(x)的最小值和最大值.
分析 (1)由x<0时,-x>0,则f(-x)=-2-x-1,再由奇函数的定义,以及性质:f(0)=0,即可得到所求函数的解析式;
(2)运用指数函数的单调性,可得x∈[0,1]时,f(x)为减函数,计算即可得到最值.
解答 解(1)由题意知,当x>0时,f(x)=-2x-1,
∴当x<0时,-x>0,则f(-x)=-2-x-1,
∵f(x)为定义在R上的奇函数,
∴f (x)=-f (-x)=2-x+1,
又∵f(x)为定义在R上的函数,
∴f(0)=0,
∴f(x)=$\left\{\begin{array}{l}{-{2}^{x}-1,x>0}\\{0,x=0}\\{{2}^{-x}+1,x<0}\end{array}\right.$;
(2)当x∈[0,1]时,解析式f(x)=-2x-1,
f(x)=-2x-1在x∈[0,1]单调递减.
当x=0时,y有最大值-2,
当x=1时,y有最小值-3.
点评 本题考查函数的奇偶性的运用:求函数的解析式,考查函数的最值的求法,注意运用函数的单调性,属于中档题.

练习册系列答案
相关题目
15.已知函数$f(x)=sinx-\sqrt{3}cosx$,则函数f(x)的图象的一条对称轴是( )
| A. | $x=\frac{5π}{6}$ | B. | $x=\frac{7π}{12}$ | C. | $x=\frac{π}{3}$ | D. | $x=\frac{π}{6}$ |
20.下列从集合A到集合B的各对应关系中,为映射的是( )
| A. | A={x|-1≤x≤1},B={x|0≤x≤2},f:x→y=|x| | B. | $A=R,B=R,f:x→y=\frac{1}{x}$ | ||
| C. | $A=R,B=R,f:x→y=\left\{\begin{array}{l}0,x≥0\\ 1,x≤0\end{array}\right.$ | D. | $A=N,B=Q,f:x→y=\sqrt{x}+1$ |
17.函数f(x)=$\frac{1}{x-1}$+lg(x+1)的定义域为( )
| A. | (-∞,-1) | B. | (1,+∞) | C. | (-1,1)∪(1,+∞) | D. | R |
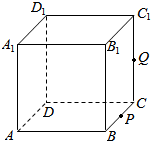 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是②④(写出所有正确命题的编号).
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是②④(写出所有正确命题的编号).