题目内容
正四棱锥所有棱长均为2,则侧棱和底面所成的角是 ( )
| A. 30° | B. 45° | C. 60 ° | D. 90° |
B
解析考点:棱锥的结构特征;与二面角有关的立体几何综合题.
专题:数形结合.
分析:先做出要求的线面角,把它放到一个直角三角形中,利用直角三角形中的边角关系求出此角.
解答: 解析:如图,四棱锥P-ABCD中,过P作PO⊥平面ABCD于O,连接AO,
解析:如图,四棱锥P-ABCD中,过P作PO⊥平面ABCD于O,连接AO,
则AO是AP在底面ABCD上的射影.∴∠PAO即为所求线面角,
∵AO= ,PA=2,
,PA=2,
∴cos∠PAO= =
= .∴∠PAO=45°,即所求线面角为45°.
.∴∠PAO=45°,即所求线面角为45°.
故选 B.
点评:本题考查棱锥的结构特征,以及求直线和平面成的角的方法,体现了数形结合的数学思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
正三棱锥的底面边长为2,侧面均为直角三角形,则此棱锥的体积为( )
A. | B. | C. | D. |
有一个几何体的三视图及其尺寸如下(单位 ),其侧视图和主视图是全等的三角形,则该几何体的表面积为
),其侧视图和主视图是全等的三角形,则该几何体的表面积为 
A. | B.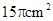 | C. | D. |
一个体积为 的正方体的顶点都在球面上,则球的体积是( )
的正方体的顶点都在球面上,则球的体积是( )
A. | B. | C. | D. |
下图是一个物体的三视图,根据图中尺寸(单位:cm),可求得该物体的体积为( )
A. cm3 cm3 | B. cm3 cm3 |
C. cm3 cm3 | D. cm3 cm3 |
 的正方形
的正方形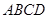 沿对角线
沿对角线 折起,使得平面
折起,使得平面 平面
平面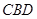 ,形成三棱锥
,形成三棱锥 的正视图与俯视图如右图所示,则侧视图的面积为
的正视图与俯视图如右图所示,则侧视图的面积为













