题目内容
有一个几何体的三视图及其尺寸如下(单位 ),其侧视图和主视图是全等的三角形,则该几何体的表面积为
),其侧视图和主视图是全等的三角形,则该几何体的表面积为 
A. | B.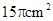 | C. | D. |
C
解析考点:由三视图求面积、体积.
专题:计算题.
分析:先由几何体还原成原来的几何体,再根据三视图中的长度关系找到几何体中的长度关系即可求解
解答:解:由三视图知原几何体为一个圆锥,底面圆的半径为3,母线长为5
∴圆锥的表面积为S=π×32+ ×2π×3×5=9π+15π=24π
×2π×3×5=9π+15π=24π
故选C
点评:本题考查三视图,由三视图求面积或体积,需根据三视图中的长度关系求出几何体中的长度关系,要求有比较好的空间想象力.属简单题

练习册系列答案
相关题目
正四棱锥所有棱长均为2,则侧棱和底面所成的角是 ( )
| A. 30° | B. 45° | C. 60 ° | D. 90° |
已知两个球的表面积之比为 ,则这两个球的半径之比为( )
,则这两个球的半径之比为( )
A. | B. | C. | D. |
下列四个几何体中,各几何体的三视图有且仅有两个视图相同的是( )
| A.①② | B.②③ | C.②④ | D.①③ |
一个正方体的顶点都在球面上,它的棱长为4cm,则球的表面积是
| A.32Лcm2 | B.48Лcm2 | C.64Лcm2 | D.80Лcm2 |
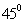 ,腰和上底均为
,腰和上底均为 的等腰梯形,那么原平面图形的面积是( )
的等腰梯形,那么原平面图形的面积是( )
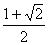

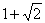




 的正三棱柱的三视图如图所示,则这个三棱柱的左视图的面积为( )
的正三棱柱的三视图如图所示,则这个三棱柱的左视图的面积为( )


 ,在该几何体的正视图中,这条棱的投影是长为
,在该几何体的正视图中,这条棱的投影是长为 的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为
的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为 和
和 的线段,则
的线段,则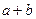 的最大值为( )
的最大值为( ) 

 W$
W$