题目内容
20.已知△ABC是边长为2的正三角形,点P为△ABC内一点,且$\overrightarrow{PA}$+2$\overrightarrow{PB}$+3$\overrightarrow{PC}$=0,则$\overrightarrow{PA}$•$\overrightarrow{PB}$=-$\frac{2}{9}$.分析 设G为BC的中点,F为AC的中点,由条件求得F、P、G共线,且PF=2PG,GF为三角形ABC的中位线.以BC所在的直线为x轴,以AG所在的直线为y轴,建立坐标系,求出点P的坐标,即可求得 $\overrightarrow{PA}$•$\overrightarrow{PB}$的值.
解答 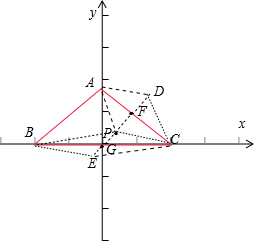 解:∵△ABC是边长为2的正三角形,且$\overrightarrow{PA}$+2$\overrightarrow{PB}$+3$\overrightarrow{PC}$=0,
解:∵△ABC是边长为2的正三角形,且$\overrightarrow{PA}$+2$\overrightarrow{PB}$+3$\overrightarrow{PC}$=0,
∴$\overrightarrow{PA}$+$\overrightarrow{PC}$=-2($\overrightarrow{PB}$+$\overrightarrow{PC}$),如图:
设G为BC的中点,F为AC的中点,APCD、BECP为平行四边形,
则有2$\overrightarrow{PF}$=-2($\overrightarrow{PG}$),即$\overrightarrow{PF}$=-2$\overrightarrow{PG}$,
∴F、P、G共线,且PF=2PG,GF为三角形ABC的中位线.
以BC所在的直线为x轴,以AG所在的直线为y轴,建立坐标系,
则点A(0,$\sqrt{3}$)、点B(-1,0),C(1,0),
故AC的中点F($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
由题意可得,$\overrightarrow{GP}$=$\frac{1}{3}$$\overrightarrow{GF}$=$\frac{1}{3}$($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)=($\frac{1}{6}$,$\frac{\sqrt{3}}{6}$),点P的坐标为($\frac{1}{6}$,$\frac{\sqrt{3}}{6}$),
∴$\overrightarrow{PA}$=(-$\frac{1}{6}$,$\frac{5\sqrt{3}}{6}$),$\overrightarrow{PB}$=(-$\frac{7}{6}$,-$\frac{\sqrt{3}}{6}$),
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$=-$\frac{1}{6}$×(-$\frac{7}{6}$)+$\frac{5\sqrt{3}}{6}$×(-$\frac{\sqrt{3}}{6}$)=-$\frac{2}{9}$.
点评 本题主要考查两个向量的加减法及其几何意义,两个向量的数量积公式,属于中档题.

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | f(2015)<[f(2015e)-f(2015)]ln2015 | B. | f(2015)>[f(2015e)-f(2015)]ln2015 | ||
| C. | f(2015)<[ef(2015)-f(2015)]ln2015 | D. | f(2015)>[ef(2015)-f(2015)]ln2015 |