题目内容
设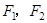 分别是椭圆:
分别是椭圆: 的左、右焦点,过
的左、右焦点,过 倾斜角为
倾斜角为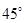 的直线
的直线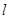 与该椭圆相交于P,
与该椭圆相交于P, 两点,且
两点,且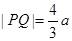 .
.
(Ⅰ)求该椭圆的离心率;
(Ⅱ)设点 满足
满足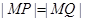 ,求该椭圆的方程.
,求该椭圆的方程.
【答案】
(1)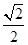 (2)
(2)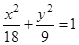
【解析】
试题分析:解:(Ⅰ)直线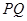 斜率为1,设直线
斜率为1,设直线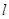 的方程为
的方程为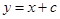 ,其中
,其中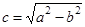 . 2分
. 2分
设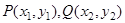 ,则
,则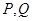 两点坐标满足方程组
两点坐标满足方程组
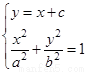 化简得
化简得 4分
4分
则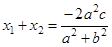 ,
,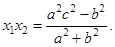
因为,所以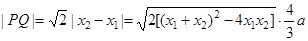 . 6分
. 6分
得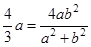 ,故
,故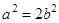 ,
,
所以椭圆的离心率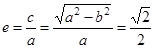 .
8分
.
8分
(Ⅱ)设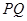 的中点为
的中点为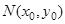 ,由(1)知
,由(1)知
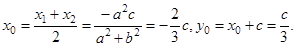 10分
10分
由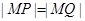 得
得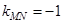 .
12分
.
12分
即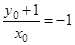 ,得
,得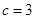 ,从而
,从而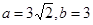 .故椭圆的方程为
.故椭圆的方程为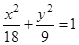 14分
14分
考点:直线与椭圆的位置关系
点评:主要是考查了直线与椭圆的位置关系的运用,属于中档题。

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目





























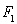
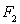
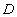
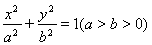
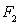
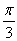
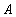
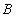
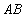
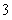
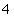
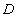
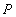
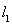
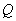
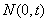
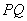
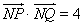
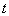
 分别是椭圆:
分别是椭圆:
 (
( )的左、右焦点,过
)的左、右焦点,过 斜率为1的直线
斜率为1的直线 与该椭圆相交于P,Q两点,且
与该椭圆相交于P,Q两点,且 ,
, ,
, 成等差数列.
成等差数列. ,
, 分别是椭圆
分别是椭圆 :
: 的左、右焦点,过
的左、右焦点,过 与
与 、
、 两点,且
两点,且 ,
, ,
, 成等差数列,
成等差数列, 满足
满足 ,求
,求