题目内容
下面是一道选择题的两种解法,两种解法看似都对,可结果并不一致,问题出在哪儿?
[题]在△ABC中,a=x,b=2,B=45°,若△ABC有两解,则x的取值范围是( )
A.(2,+∞)B.(0,2)C.(2, 2
)D.(
, 2)
[解法1]△ABC有两解,asinB<b<a,xsin45°<2<x,即2<x<2
,故选C.
[解法2]
=
,sinA=
=
=
.
△ABC有两解,bsinA<a<b,2×
<x<2,即0<x<2,故选B.
你认为______是正确的 (填“解法1”或“解法2”)
[题]在△ABC中,a=x,b=2,B=45°,若△ABC有两解,则x的取值范围是( )
A.(2,+∞)B.(0,2)C.(2, 2
| 2 |
| 2 |
[解法1]△ABC有两解,asinB<b<a,xsin45°<2<x,即2<x<2
| 2 |
[解法2]
| a |
| sinA |
| b |
| sinB |
| asinB |
| b |
| xsin45° |
| 2 |
| ||
| 4 |
△ABC有两解,bsinA<a<b,2×
| ||
| 4 |
你认为______是正确的 (填“解法1”或“解法2”)
解法1正确
∵若a<b,则A<B,∵B=45°,∴△ABC只有一解,故解法2不正确
故答案为:解法1
∵若a<b,则A<B,∵B=45°,∴△ABC只有一解,故解法2不正确
故答案为:解法1

练习册系列答案
相关题目
下面是一道选择题的两种解法,两种解法看似都对,可结果并不一致,问题出在哪里
?在△ABC中,a=x,b=2,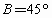 ,若△ABC有两解,则x的取值范围是
,若△ABC有两解,则x的取值范围是
[
]|
A .(2,+∞) |
B .(0,2) |
C .(2,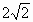 ) ) |
D .(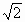 ,2) ,2) |
解法
1 △ABC有两解,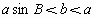 ,
,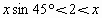 ,
,
即
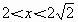 ,故选C.
,故选C.
解法
2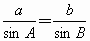 ,
,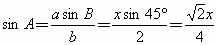 .
.
△
ABC有两解,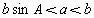 ,
,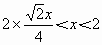 ,即0<x<2,故选B.
,即0<x<2,故选B.  D.
D.
 ,故选C.
,故选C. ,
, .
. ,即0<x<2,故选B.
,即0<x<2,故选B.