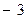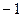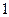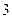题目内容
已知向量
,
,
,是空间的一个单位正交基底,若向量
在基底
,
,
下的坐标为(2,1,3),那么向量
在基底
+
,
-
,
下的坐标为( )
| a |
| b |
| c |
| P |
| a |
| b |
| c |
| P |
| a |
| b |
| a |
| b |
| c |
A.(-
| B.(-
| C.(
| D.(
|
由题意向量
=2
+
+3
,设向量
在基底
+
,
-
,
下的坐标为(x,y,z),
∴
=x(
+
)+y(
-
)+z
,
所以2
+
+3
=x(
+
)+y(
-
)+z
,可得:
,∴x=
,y=
,z=3.
向量
在基底
+
,
-
,
下的坐标为(
,
,3).
故选C.
| P |
| a |
| b |
| c |
| P |
| a |
| b |
| a |
| b |
| c |
∴
| P |
| a |
| b |
| a |
| b |
| c |
所以2
| a |
| b |
| c |
| a |
| b |
| a |
| b |
| c |
|
| 3 |
| 2 |
| 1 |
| 2 |
向量
| P |
| a |
| b |
| a |
| b |
| c |
| 3 |
| 2 |
| 1 |
| 2 |
故选C.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
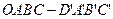 中,
中,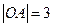 ,
,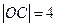 ,
,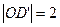 .写出
.写出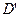 ,
,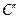 ,
,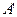 ,
,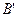 四点的坐标.
四点的坐标.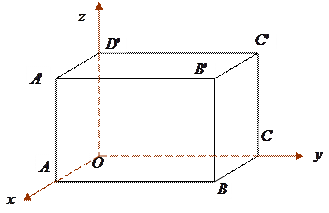
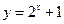 的图象按向量
的图象按向量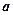 平移得到函数
平移得到函数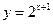 的
的 .
.
 是两个非零向量,且
是两个非零向量,且 ,则
,则 与
与 的夹角为( )
的夹角为( )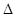 OAB中,点A是BC的中点,点D是将向量
OAB中,点A是BC的中点,点D是将向量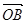 分为2:1的一个分点,DC和OA交于点E.设
分为2:1的一个分点,DC和OA交于点E.设 ,
,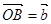
 表示
表示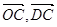 ;
;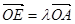 ,求实数
,求实数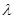 的值.
的值. 中,
中,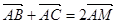 ,
, 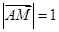 ,点
,点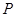 在
在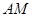 上且满足
上且满足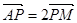 ,则
,则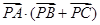 等于( )
等于( )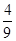
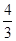

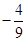
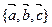 是空间一个
是空间一个 基底,则一定可以与向量
基底,则一定可以与向量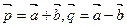
 构成空间的另一个基底的向量是
构成空间的另一个基底的向量是



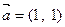 ,
,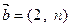 ,若
,若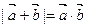 ,则
,则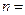 ( )
( )