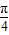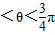题目内容
设0≤θ<2π,如果sinθ<0且cos2θ<0,则θ的取值范围是( )
A、π<θ<
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:根据正弦小于零和角的范围,可以判断角在第三、四象限,由二倍角的余弦值小于零,得1-2sin2θ<0,得到sinθ>
或sinθ<-
,解得θ的范围,与上面范围求交集.
| ||
| 2 |
| ||
| 2 |
解答:解:∵0≤θ<2π,sinθ<0,
∴π<θ<2π,
∵cos2θ<0,
∴1-sin2θ<0,
∴sinθ>
或sinθ<-
,
∴
<θ<
或
<θ<
,
综上可知
<θ<
,
故选D
∴π<θ<2π,
∵cos2θ<0,
∴1-sin2θ<0,
∴sinθ>
| ||
| 2 |
| ||
| 2 |
∴
| π |
| 4 |
| 3π |
| 4 |
| 5π |
| 4 |
| 7π |
| 4 |
综上可知
| 5π |
| 4 |
| 7π |
| 4 |
故选D
点评:本题涉及到三角函数符号问题,根据所给的三角函数的符号,确定角的范围,同时又用到二倍角公式,由二倍角公式变形整理得单角的三角函数范围,从而确定角的范围.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 π<θ<
π<θ< π
π π<θ<2π
π<θ<2π
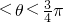
 π<θ<
π<θ< π
π π<θ<2π
π<θ<2π π
π