题目内容

函数f（x）的图象经过原点，且它的导函数y=f′（x）是如图所示的一条直线，则函数y=f（x）的图象的顶点在（　　）
分析：根据导函数的图象判断函数的单调性，再结合f（x）的图象经过原点，就可判断函数y=f（x）的图象的顶点的位置．
解答：解：∵导数的正负决定了原函数的单调性，导数取 0时，函数有极值．
∴根据图象可，当x＜a时，导数大于0，为增函数，当x＞a时，导数小于0，为减函数，
当x=a时，导数等于0，函数有极值，
∵由图可知，a＞0，∴函数y=f（x）的图象的顶点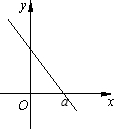应该在第一象限或第三象限
又∵f（x）的图象经过原点，∴f（x）的图象的顶点在第一象限．
故选A
点评：本题主要考查借助导函数的图象，根据图象观察导函数的正负，来判断原函数的图象．
练习册系列答案
相关题目
8、若把函数y=f（x）的图象作平移，可以使图象上的点P（1，0）变换成点Q（2，2），则函数y=f（x）的图象经此变换后所得图象对应的函数为
y=f（x-1）+2
．
8、若把函数y=f（x）的图象作平移，可以使图象上的点P（1，0）变换成点Q（2，2），则函数y=f （x）的图象经此变换后所得图象对应的函数为（　　）
（2012•福建模拟）设函数f（x）的图象是由函数g(x)=cos2x+
3
sinxcosx-
1
2
的图象经下列两个步骤变换得到：
（1）将函数g（x）的图象向右平移
π
12
个单位，并将横坐标伸长到原来的2倍（纵坐标不变），得到函数h（x）的图象；
（2）将函数h（x）的图象上各点的纵坐标缩短为原来的m(0＜m＜
1
2
)倍（横坐标不变），并将图象向上平移1个单位，得到函数f（x）的图象．
（Ⅰ）求f（x）的表达式；
（Ⅱ）判断方程f（x）=x的实根的个数，证明你的结论；
（Ⅲ）设数列{an}满足a1=0，an+1=f（an），试探究数列{an}的单调性，并加以证明．
若把函数y=f（x）的图象作平移，可以使图象上的点P（1，0）变换成点Q（2，2），则函数y=f （x）的图象经此变换后所得图象对应的函数为（ ）
A．y=f（x-1）+2
B．y=f（x-1）-2
C．y=f（x+1）+2
D．y=f（x+1）-2
若把函数y=f（x）的图象作平移，可以使图象上的点P（1，0）变换成点Q（2，2），则函数y=f （x）的图象经此变换后所得图象对应的函数为（ ）
A．y=f（x-1）+2
B．y=f（x-1）-2
C．y=f（x+1）+2
D．y=f（x+1）-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网