Question

【题目】若为定义域上的单调函数,且存在区间（其中,使得当时, 的取值范围恰为,则称函数是上的“优美函数”.

函数是否为“优美函数”？若是,求出的值；若不是，请说明理由.

若为“优美函数”，求实数的取值范围.

若函数为“优美函数”，求实数的取值范围.

Answer 1

【答案】（1）是“优美函数”,过程见解析

（2）

（3）

【解析】

（1）由已知条件中“优美函数”的定义，说明函数在区间的值域是，又由函数的单调性，得到关于的方程，解出即可；
（2）由题意知，函数为“优美函数”，等价于方程有两实根，利用判别式和韦达定理列不等式，解不等式可得的范围；

（3）函数为“优美函数”，可得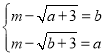，消去，可得间的关系，再代入原方程组，可得两个结构一摸一样的方程，将方程组的问题化归为一个二次方程有两正根的问题，利用判别式和韦达定理列不等式，解不等式可得的范围．

解：因为函数在区间上单调递增，且值域为,

，

，

，

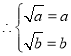所以是“优美函数”,此时,；

因为函数为递增函数,

要使在定义域区间上存在,使得的值域,

则只需有两个不等的实根,

由得在有两个不等的实根,设为，

，

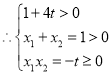解得；

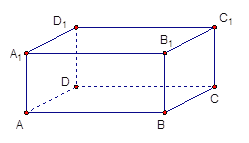
因为函数在上单调递减，

由题意得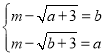，两式相减，

得，

可得

将上式代入方程组得，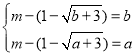

是方程的两根，

令在上有两个不同的实根，设为，

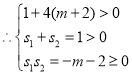
解得．