在平行四边形ABCD中.BM⊥AC于M点.BM=2.N是△ABC边界及内部的任意一点.$\overrightarrow{BM}•\overrightarrow{BN}$的取值范围是[0.4]．题目和参考答案——青夏教育精英家教网—

题目内容

2．在平行四边形ABCD中，BM⊥AC于M点，BM=2，N是△ABC边界及内部的任意一点，$\overrightarrow{BM}•\overrightarrow{BN}$的取值范围是[0，4]．

分析设$\overrightarrow{BN}$在$\overrightarrow{BM}$上的投影为BN'，由向量的数量积的几何意义，只要求得BN'的最小值和最大值，即可得到所求范围．

解答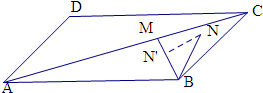解：设$\overrightarrow{BN}$在$\overrightarrow{BM}$上的投影为BN'，
$\overrightarrow{BM}•\overrightarrow{BN}$=|$\overrightarrow{BM}$|•|$\overrightarrow{BN}$|cos∠MBN
=2|$\overrightarrow{BN}$|cos∠MBN=2BN'，
由线段BN'最小值为0，最大值为2，
可得$\overrightarrow{BM}•\overrightarrow{BN}$的最小值为0，最大值为4．
即有$\overrightarrow{BM}•\overrightarrow{BN}$的取值范围是[0，4]，
故答案为：[0，4]．

点评本题考查向量的数量积的定义及几何意义，考查运算能力，属于基础题．

练习册系列答案

13．作出下列函数的图象．并研究它们的单调区间：
（1）f（x）=（x+1）²+2；
（2）f（x）=-2x²；
（3）f（x）=$\sqrt{{x}^{2}+1}$；
（4）f（x）=x²-x．

10．不等式-x²+3x+4＜0的两边同时乘以-1可得（　　）

17．

函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的部分图象如图所示．
（1）求f（x）的解析式；
（2）设g（x）=[f（x-$\frac{π}{12}$）]²，求函数g（x）在x∈[-$\frac{π}{6}$，$\frac{π}{3}$]上的最大值，并确定此时x的值．

7．下列命题正确的是（　　）

	A．	y=sinx的递增区间是[2kπ，2kπ+$\frac{π}{2}$]（k∈Z）
	B．	y=sinx在第一象限是增函数
	C．	y=sinx在[-$\frac{π}{2}，\frac{π}{2}$]上是增函数
	D．	y=sinx关于点（$\frac{π}{2}$，1）中心对称

14．设P为不等式组$\left\{\begin{array}{l}{（2+\sqrt{3}）x-y-1≥0}\\{x+y-1≤0}\\{y≥0}\end{array}\right.$所表示的区域内任意一点，过P作圆（x-2）²+（y-1）²=1的切线，切点为A，B，则∠APB的取值范围是（　　）

A．

[$\frac{π}{6}$，$\frac{π}{3}$]

B．

[$\frac{π}{6}$，$\frac{π}{4}$]

C．

[$\frac{π}{4}$，$\frac{π}{2}$]

D．

[$\frac{π}{3}$，$\frac{π}{2}$]

11．已知函数f（r）=$\frac{x+2}{x-6}$，则[f（f（14）]=-1；f（x）=3，则x=10．

12．已知x＜0，求y=$\frac{1+{x}^{2}}{x}$的最大值．

试题分类