题目内容
数列{
}的前n项和为
，
（Ⅰ）设
，证明：数列｛
｝是等比数列；
（Ⅱ）求数列
的前n项和
；
（Ⅲ）若
，
，
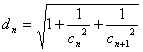，求不超过P的最大整数的值。
解:(Ⅰ) 因为
，
所以 ① 当
时，
，则
，
② 当
时，
，
所以
，即
，
所以
，而
，
所以数列
是首项为
，公比为的等比数列，所以
．
（Ⅱ） 由(Ⅰ)得
．
所以 ①
②
②-①得：
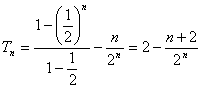
（Ⅲ）由(Ⅰ)知
而
，………………（11分）
所以
，
故不超过
的最大整数为
．
练习册系列答案
相关题目