题目内容
已知各项均为正数的数列{an}的前n项和为Sn,函数f(x)=
px2一(p+q)x+qlnx(其中p,q均为常数,且p>q>0),当x=a1时,函数f(x)取得极小值,点(an,2Sn)(n∈N*)均在函数y=2px2-
+f'(x)+q的图象上.(其中f'(x)是函数f(x)的导函数)
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)记bn=
•qn,求数列{bn}的前n项和Tn.
| 1 |
| 2 |
| q |
| x |
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)记bn=
| 4Sn |
| n+3 |
分析:(1)先对函数f(x)进行求导,令其导数为0求得x,进而根据x变化时f'(x)和f(x)的变化情况确定函数f(x)的极小值,求得a1;
(2)依题意可知点(an,2sn)代入解析式,再由a1的值求出p,求得2Sn=2an2+an-1,进而利用an=sn-sn-1,求得数列的递推式,整理求得an-an-1-
=0,推断出数列为等差数列,利用等差数列通项公式求得an;
(3)根据题意和(2)结论求出Sn,再求出bn,根据特点利用错位相减法求出数列{bn}的前n项和Tn,需要说明q≠1.
(2)依题意可知点(an,2sn)代入解析式,再由a1的值求出p,求得2Sn=2an2+an-1,进而利用an=sn-sn-1,求得数列的递推式,整理求得an-an-1-
| 1 |
| 2 |
(3)根据题意和(2)结论求出Sn,再求出bn,根据特点利用错位相减法求出数列{bn}的前n项和Tn,需要说明q≠1.
解答:解:(1)由题意得,函数f(x)的定义域为(0,+∞),
f′(x)=px-(p+q)+
=
=
令f′(x)=0,得x=1或x=
,
∵p>q>0,∴0<
<1,
当x变化时,f'(x)和f(x)的变化情况如下表:
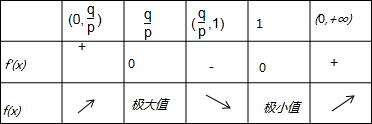
∴f(x)处取得极小值,即a1=1.
(2)依题意,y=2px2-
+f′(x)+q=2px2+px-p,
∵点(an,2Sn)(n∈N*)均在函数y=2px2-
+f′(x)+q图象上,
∴2Sn=2p•an2+p•an-p,
则2a1=2pa12+pa1-p,由a1=1求得p=1
∴2Sn=2an2+an-1
当n≥2时,2Sn-1=2an-12+an-1-1
两式相减求得(an+an+1)(an-an-1-
)=0,
∵an+an+1>0,∴an-an-1-
=0
∴数列{an}是以1为首项,
为公差的等差数列,
∴an=1+(n-1)×
=
,
(3)由(2)得,2Sn=2an2+an-1=2×(
)2+
-1,
解得Sn=
,∴bn=
•qn=nqn,
则Tn=1×q1+2×q2+…+n•qn③
又qTn=1×q2+2×q3+…+(n-1)•qn+n•qn+1 ④
∵p>q>0,且由(2)知p=1,∴q≠1,
③-④得,(1-q)Tn=q1+q2+q3+…+qn-n•qn+1=
-n•qn+1
∴Tn=
-
.
f′(x)=px-(p+q)+
| q |
| x |
| px2-(p+q)x+q |
| x |
| (x-1)(px-q) |
| x |
令f′(x)=0,得x=1或x=
| q |
| p |
∵p>q>0,∴0<
| q |
| p |
当x变化时,f'(x)和f(x)的变化情况如下表:

∴f(x)处取得极小值,即a1=1.
(2)依题意,y=2px2-
| q |
| x |
∵点(an,2Sn)(n∈N*)均在函数y=2px2-
| q |
| x |
∴2Sn=2p•an2+p•an-p,
则2a1=2pa12+pa1-p,由a1=1求得p=1
∴2Sn=2an2+an-1
当n≥2时,2Sn-1=2an-12+an-1-1
两式相减求得(an+an+1)(an-an-1-
| 1 |
| 2 |
∵an+an+1>0,∴an-an-1-
| 1 |
| 2 |
∴数列{an}是以1为首项,
| 1 |
| 2 |
∴an=1+(n-1)×
| 1 |
| 2 |
| n+1 |
| 2 |
(3)由(2)得,2Sn=2an2+an-1=2×(
| n+1 |
| 2 |
| n+1 |
| 2 |
解得Sn=
| n2+3n |
| 4 |
| 4Sn |
| n+3 |
则Tn=1×q1+2×q2+…+n•qn③
又qTn=1×q2+2×q3+…+(n-1)•qn+n•qn+1 ④
∵p>q>0,且由(2)知p=1,∴q≠1,
③-④得,(1-q)Tn=q1+q2+q3+…+qn-n•qn+1=
| q(1-qn) |
| 1-q |
∴Tn=
| q(1-qn) |
| (1-q)2 |
| nqn+1 |
| 1-q |
点评:本题考查了数列与函数的综合,涉及了函数的导数求极值,数列前n项和与数列通项公式的关系,以及错位相减法求数列的前n项和,考查分析解决问题的能力和运算能力.

练习册系列答案
相关题目
 与
与 的大小,并加以证明.
的大小,并加以证明. 与
与 的大小,并加以证明.
的大小,并加以证明. 与
与 的大小,并加以证明.
的大小,并加以证明.