题目内容
（2012•佛山一模）已知点P是抛物线x2=4y上的一个动点，则点P到点M（2，0）的距离与点P到该抛物线准线的距离之和的最小值为（ ）
分析：利用抛物线的定义，将抛物线x2=4y上的点P到该抛物线准线的距离转化为点P到其焦点F的距离，当F、P、M共线时即可满足题意，从而可求得距离之和的最小值．
解答：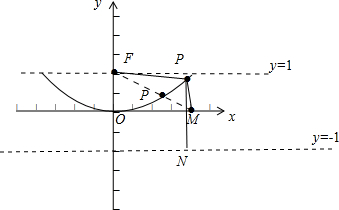
解：∵抛物线x2=4y的焦点F的坐标为F（0，1），作图如下，
∵抛物线x2=4y的准线方程为y=-1，设点P到该抛物线准线y=-1的距离为d，
由抛物线的定义可知，d=|PF|，
∴|PM|+d=|PM|+|PF|≥|FM|（当且仅当F、P、M三点共线时（P在F，M中间）时取等号），
∴点P到点M（2，0）的距离与点P到该抛物线准线的距离之和的最小值为|FM|，
∵F（0，1），M（2，0），△FOM为直角三角形，
∴|FM|=
，
故选B．
解：∵抛物线x2=4y的焦点F的坐标为F（0，1），作图如下，∵抛物线x2=4y的准线方程为y=-1，设点P到该抛物线准线y=-1的距离为d，
由抛物线的定义可知，d=|PF|，
∴|PM|+d=|PM|+|PF|≥|FM|（当且仅当F、P、M三点共线时（P在F，M中间）时取等号），
∴点P到点M（2，0）的距离与点P到该抛物线准线的距离之和的最小值为|FM|，
∵F（0，1），M（2，0），△FOM为直角三角形，
∴|FM|=
| 5 |
故选B．
点评：本题考查抛物线的简单性质，着重考查抛物线的定义的应用，突出转化思想的运用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
（2012•佛山一模）如图，三棱锥P-ABC中，PB⊥底面ABC，∠BCA=90°，PB=BC=CA=2，E为PC的中点，点F在PA上，且2PF=FA．