Question

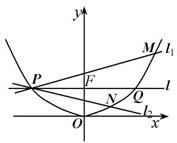已知抛物线C：x²=2py（p为正常数）的焦点为F，过F做一直线l交C于P，Q两点，点O为坐标原点．
（1）若△POQ的面积记为S，求

S2

|PQ|

的值；
（2）若直线l垂直于y轴，过点Q做关于直线l的对称的两条直线l₁，l₂分别交抛物线C于M，N两点，证明：直线MN斜率等于抛物线在点Q处的切线斜率．

Answer 1

分析：（1）显然直线l斜率存在，F(0，

p

2

)，设l：y=kx+

p

2

代入代入抛物线的方程，消去y得到关于x的一元二次方程，再结合根系数的关系利用弦长公式即可求得求

S2

|PQ|

的值，从而解决问题．
（2）不妨设P(-p，

p

2

)，Q(p，

p

2

)，利用直线与抛物线的交点坐标求得点M，N的坐标x_M，x_N再利用直线的斜率公式求出直线MN的斜率，及抛物线在点Q处的切线斜率即可得到证明．

解答：解（1）显然直线l斜率存在，F(0，

p

2

)
设l：y=kx+

p

2

代入C：x²=2py得x²-2pkx-p²=0，x₁+x₂=2pk，x₁x₂=-p²，（2分）
求得弦长|PQ|=2p（1+k²），原点到直线l距离

p

2 1+k2

，（2分）
S2=

1

4

•(

p

2 1+k2

)2|PQ|2，所以

S2

|PQ|

=

p3

8

（2分）
（2）不妨设P(-p，

p

2

)，Q(p，

p

2

)，
设l1：y=k1(x+p)+

p

2

代入C：x²=2py
得x²-2pk₁x-2p²k₁-p²=0，x_Px_M=-2k₁p²-p²，
所以x_M=2k₁p+p，同理x_N=2k₂p+p，（2分）k₁+k₂=0，
kMN=

yM-yN

xM-xN

=

xM+xN

2p

=1，（2分）
抛物线在点Q处的切线斜率y′=

2x

2p

|x=p=1=kMN，得证（2分）

点评：当直线与圆锥曲线相交时，涉及弦长问题，常用“韦达定理法”设而不求计算弦长（即应用弦长公式）；涉及弦长的中点问题，常用“点差法”设而不求，将弦所在直线的斜率、弦的中点坐标联系起来，相互转化，同时还应充分挖掘题目的隐含条件，寻找量与量间的关系灵活转化，往往就能事半功倍．