题目内容
(本小题满分12分)
在△ABC中,内角A、B、C所对边的长分别为a、b、c,已知向量 =(1,cosA -1),
=(1,cosA -1), =(cosA,1)且满足
=(cosA,1)且满足 ⊥
⊥ .
.
(Ⅰ)求A的大小;
(Ⅱ)若a= ,b+c=3 求b、c的值.
,b+c=3 求b、c的值.
【答案】
(1) A=60º ;(2) 
【解析】
试题分析:(1)根据已知中 ,化简得到cosA的值,进而得到角A.
,化简得到cosA的值,进而得到角A.
(2)由余弦定理a2=b2+c2-2bccosA得a2=(b+c)2-2bc-2bccosA,进一步得到c+b的值。
(1) ,cosA=
,cosA= ,A为△ABC内角,∴A=60º
,A为△ABC内角,∴A=60º
(2)a=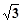 ,A=60º,由余弦定理
,A=60º,由余弦定理
a2=b2+c2-2bccosA得a2=(b+c)2-2bc-2bccosA
∵b+c=3, ∴3=9-3bc,bc=2
由 得
得
考点:本试题主要考查了两个向量两个向量共线的性质,已知三角函数值求角,以及三角形中余弦定理的应用.
点评:解决该试题的关键是向量垂直的充要条件的运用,数量积为零,得到角A的值,然后在此 基础上进一步运用余弦定理得到求解。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目