题目内容
若函f(x)=x3-3x+a有3个不同的零点,则实数a的取值范围是
| A.(-2,2) | B.[-2,2] | C.(-∞,-1) | D.(1,+∞) |
A
解:设g(x)=x3,h(x)=3x-a
∵f(x)=x3-3x+a有三个不同零点,即g(x)与h(x)有三个交点
∵g'(x)=3x2,h'(x)=3
当g(x)与h(x)相切时
g'(x)=h'(x),3x2=3,得x=1,或x=-1
当x=1时,g(x)=1,h(x)=3-a=1,得a=2
当x=-1时,g(x)=-1,h(x)=-3-a=-1,得a=-2
要使得g(x)与h(x)有三个交点,则-2<a<2
故答案为:-2<a<2,选A
∵f(x)=x3-3x+a有三个不同零点,即g(x)与h(x)有三个交点
∵g'(x)=3x2,h'(x)=3
当g(x)与h(x)相切时
g'(x)=h'(x),3x2=3,得x=1,或x=-1
当x=1时,g(x)=1,h(x)=3-a=1,得a=2
当x=-1时,g(x)=-1,h(x)=-3-a=-1,得a=-2
要使得g(x)与h(x)有三个交点,则-2<a<2
故答案为:-2<a<2,选A

练习册系列答案
相关题目
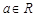 ,函数
,函数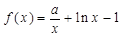 ,
,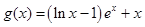 (其中
(其中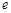 为自然对数的底数).
为自然对数的底数).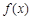 在
在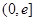 上的单调性;
上的单调性;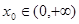 ,使曲线
,使曲线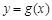 在点
在点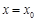 处的切线与
处的切线与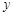 轴垂直? 若存在,
轴垂直? 若存在,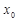 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;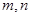 满足
满足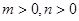 ,求证:
,求证: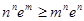 .
. 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为



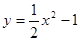 在点
在点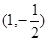 处切线的倾斜角为( )
处切线的倾斜角为( )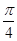


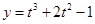 ,当
,当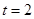 s时,物体的瞬时速度v等于 ( )
s时,物体的瞬时速度v等于 ( )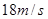
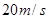
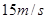
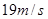
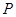 在曲线
在曲线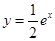 上,点
上,点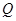 在曲线
在曲线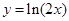 上,则
上,则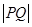 最小值为( )
最小值为( )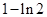
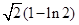
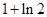
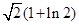
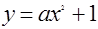 ,该曲线
,该曲线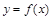 以点
以点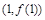 处的切线平行于直线
处的切线平行于直线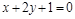 ,则该曲线的切线方程 .
,则该曲线的切线方程 .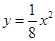 的一条切线的斜率为
的一条切线的斜率为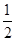 ,则切点的横坐标为( )
,则切点的横坐标为( )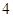
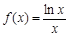 单调增区间是 ;
单调增区间是 ;