题目内容
一个正方体内接于一个高为
,底面半径为1的圆锥,则正方体的棱长为
.
| 2 |
| ||
| 2 |
| ||
| 2 |
分析:作出过正方体的体对角线作圆锥的轴截面,设正方体的棱长为x,通过三角形相似,求出正方体的棱长即可.
解答: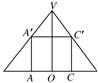 解:如图,过正方体的体对角线作圆锥的轴截面,设正方体的棱长为x,
解:如图,过正方体的体对角线作圆锥的轴截面,设正方体的棱长为x,
则OC=
x,∴
=
,
解得x=
,
∴正方体的棱长为
,
故答案为:
.
 解:如图,过正方体的体对角线作圆锥的轴截面,设正方体的棱长为x,
解:如图,过正方体的体对角线作圆锥的轴截面,设正方体的棱长为x,则OC=
| ||
| 2 |
| ||||
| 1 |
| ||
|
解得x=
| ||
| 2 |
∴正方体的棱长为
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题是基础题,正确作出图形,注意到过正方体的体对角线作圆锥的轴截面,AC是正方体的面对角线,三角形相似.考查空间想象能力,计算能力好题,常考题型.

练习册系列答案
相关题目


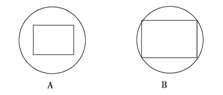
 (理科)一个正方体内接于一个球,过球心作一截面,则截面可能的图形是( )
(理科)一个正方体内接于一个球,过球心作一截面,则截面可能的图形是( )