题目内容
已知 为椭圆
为椭圆 上的一点,
上的一点, 分别为圆
分别为圆 和圆
和圆 上的点,则
上的点,则 的最小值为( )
的最小值为( )
| A.5 | B.7 | C.13 | D.15 |
B
解析试题分析:依题意可得,椭圆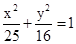 的焦点分别是两圆(x+3)2+y2=1和(x-3)2+y2=4的圆心,(-3,0),(3,0),所以根据椭圆的定义P到两焦点的距离和始终为2a=10,那么可得:(|PM|+|PN|)min=2×5-1-2=7,
的焦点分别是两圆(x+3)2+y2=1和(x-3)2+y2=4的圆心,(-3,0),(3,0),所以根据椭圆的定义P到两焦点的距离和始终为2a=10,那么可得:(|PM|+|PN|)min=2×5-1-2=7,
故选B.
考点:本试题主要考查了圆的性质及其应用,以及椭圆的定义,解题时要认真审题,仔细解答,注意公式的合理运用.
点评:解决该试题的关键是求解距离的最小值问题,理解两圆的圆心是椭圆的焦点,那么结合椭圆的定义和圆的性质可得。

练习册系列答案
相关题目
如果方程 表示焦点在
表示焦点在 轴上的椭圆,则
轴上的椭圆,则 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
 是椭圆
是椭圆 的两个焦点,
的两个焦点, 为椭圆上一点,且
为椭圆上一点,且 ,则
,则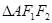 的面积为
的面积为
| A.7 | B. | C. | D. |
双曲线 的焦距是
的焦距是
| A.4 | B. | C.8 | D.与 有关 有关 |
抛物线 的焦点到准线的距离是 ( )
的焦点到准线的距离是 ( )
A.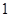 | B. | C.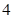 | D. |
过点 且与双曲线
且与双曲线 -y
-y =1有公共渐近线的双曲线方程是( )
=1有公共渐近线的双曲线方程是( )
A. - -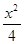 =1 =1 | B. - - =1 =1 |
C.y - - =1 =1 | D. - -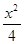 =1或 =1或 - - =1 =1 |
椭圆 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
椭圆 的离心率是( )
的离心率是( )
A. | B.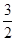 | C. | D. |
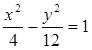 ,则它的一个焦点到一条渐进线的距离是( )
,则它的一个焦点到一条渐进线的距离是( )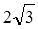 D. 12
D. 12