题目内容
平面ABCD中,点A坐标为(0,1,1),点B坐标为(1,2,1),点C坐标为(-1,0,-1).若向量
=(-2,y,z),且
为平面ABC的法向量,则yz=( )
| a |
| a |
分析:由向量
=(-2,y,z),且
为平面ABC的法向量,根据法向量与平面内任何一个向量都垂直,数量积均为0,构造方程组,然后逐一分析四个答案中的向量,即可找到满足条件的答案.
| a |
| a |
解答:解:
=(1,1,0),
=(-1,-1,-2),
与平面ABC垂直的向量应与上面的向量的数量积为零,
向量
=(-2,y,z),且
为平面ABC的法向量,
则
⊥
且
⊥
,即
•
=0,且
•
=0,即
-2+y+0=0且2-y-2z=0,
即
,
∴则yz=20=1,
故选C.
| AB |
| AC |
与平面ABC垂直的向量应与上面的向量的数量积为零,
向量
| a |
| a |
则
| a |
| AB |
| a |
| AC |
| a |
| AB |
| a |
| AC |
-2+y+0=0且2-y-2z=0,
即
|
∴则yz=20=1,
故选C.
点评:本题考查的知识点是向量语言表述线线的垂直、平行关系,其中根据法向量与平面内任何一个向量都垂直,数量积均为0,构造方程组,是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在复平面内的?ABCD中,点A,B,C分别对应复数4+i,3+4i,3-5i,则点D对应的复数是( )
| A、2-3i | B、4+8i | C、4-8i | D、1+4i |
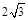 的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=
的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=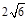 ,M,N分别为PB,PD的中点.
,M,N分别为PB,PD的中点.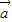 =(-2,y,z),且
=(-2,y,z),且 为平面ABC的法向量,则yz=( )
为平面ABC的法向量,则yz=( )